Question

Handelt es sich hier um eine Flächenbilanz?

Ja? Nein? -Warum

Answer 1

Nein.

Die Funktion hat eine Nullstelle bei 2, verläuft also im Integrationsbereich
über- und  unterhalb der x-Achse.

Die Fläche wäre
Integral zwischen 0 und 2 plus
Integral zwischen 2 und 3

Beides als Betrag addiert.

~plot~ 2 - 0.5 * x^2 ~plot~

Comments

Doch es handelt sich um eine Bilanz

---

Die Fläche wäre
Integral zwischen 0 und 2 plus
Integral zwischen 2 und 3
DAs zeigt doch das es eine ist.

---

Stell dir einmal die sin-Funktion von
0 bis 2*π vor.
Dies ist einmal oberhalb der x-Achse und einmal
unterhalb der x-Achse.

Das Integral der sin-Funktion zwischen 0 und 2 * π ist NULL
Beide Flächen heben sich auf.

Die Fläche 0 bis π  und π bis 2*π
ist ungleich 0.

Falls du anderer Ansicht bist habe ich nichts dagegen.

---

Das Wort " Flächenbilanz " habe ich bisher im Zusammenhang mit
Integralrechnung noch nicht vernommen.

Im kaufmännischen gibt es wohl die " Bilanz " ( bin allerdings
kein Kaufmann ) beider plus und minus zu Gewinn oder Verlust
verrechnet werden.

Von daher könnte die Analogie zum Integral gegeben sein.

Da Flächen immer positiv sind müßte ein negativer Integralwert
noch mit abs ( ) bzw. Betrag in die Fläche umgerechnet werden.

|  ∫ term dx | als Fläche.

Answer 2

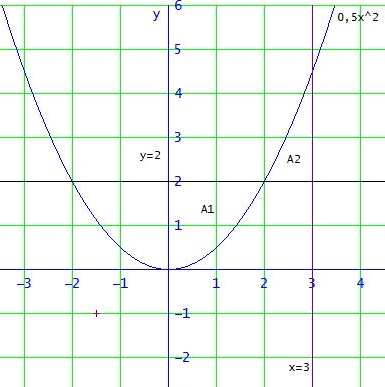
₀∫² ( 2 - 0,5x²) dx  gibt die Fläche A1 an,   ₂∫³ ( 2 - 0,5x²) dx   die negative Maßzahl der Fläche A1

Es handelt sich also eher nicht um ein Flächenbilanz, denn das ₀∫³ ( 2 - 0,5x²) dx gibt die Flächendifferenz A1 - A2 an, also keine "sichtbare" Flache

[ könnte man natürlich auch "Flächenbilanz" nennen, "Bilanz" könnte so gemeint so gemeint ]

Gruß Wolfgang

Comments

der Graph ist bei dir falsch

---

Nicht, wenn du die Funktionsgleichung liest, die oben rechts an dem Graph steht !  :-)

A1 und A2 sind Teilflächen zwischen den Graphen f(x) = 0,5x² und g(x) = 2

über den Intervallen [0;2] und [2;3]