Wahrscheinlichkeitsmassefunktion erklären

Question

Aufgabe:

Wahrscheinlichkeitsmassefunktion
Eine Funktion \( p: \Omega \rightarrow[0,1] \) heißt Wahrscheinlichkeitsmassefunktion ( \( p m f \), probability mass function) einer Verteilung \( P \) auf \( \Omega \), wenn für alle \( \omega \in \Omega \) gilt: \( p(\omega)=P(\omega) \).
Sie ist die Wahrscheinlichkeit der diskreten Zufallsvariablen, also für jede diskrete Zufallsvariablen \( x_{1}, x_{2}, x_{3}, \ldots, x_{k} \) die entsprechenden Wahrscheinlichkeiten \( P\left(x_{1}\right), P\left(x_{2}\right), P\left(x_{3}\right), P\left(x_{4}\right), \ldots, P\left(x_{k}\right) \) sind die entsprechenden Wahrscheinlichkeitsmassefunktionen.
Insbesondere für \( X=a \) ist \( P(X=a) \) seine pmf.

Problem/Ansatz:

Kann mir das Jemand vielleicht erklären? Am meisten verwirrt mich, was der Unterschied zwischen p und P sein soll.

Answer 1

Eine Wahrscheinlichkeitsmassefunktion \(p\) für eine diskrete Zufallsvariable \(X\), die die Werte \(\Omega=\{x_1,...,x_n\}\) hat, ordnet jedem dieser \(x_i\) seine Wahrscheinlichkeitsmasse zu ("Punktmassen").

Bei Wahrscheinlichkeiten summieren sich diese Punktmassen zu \(1\).

Hier mal ein paar mögliche Verteilungsweisen der Masse: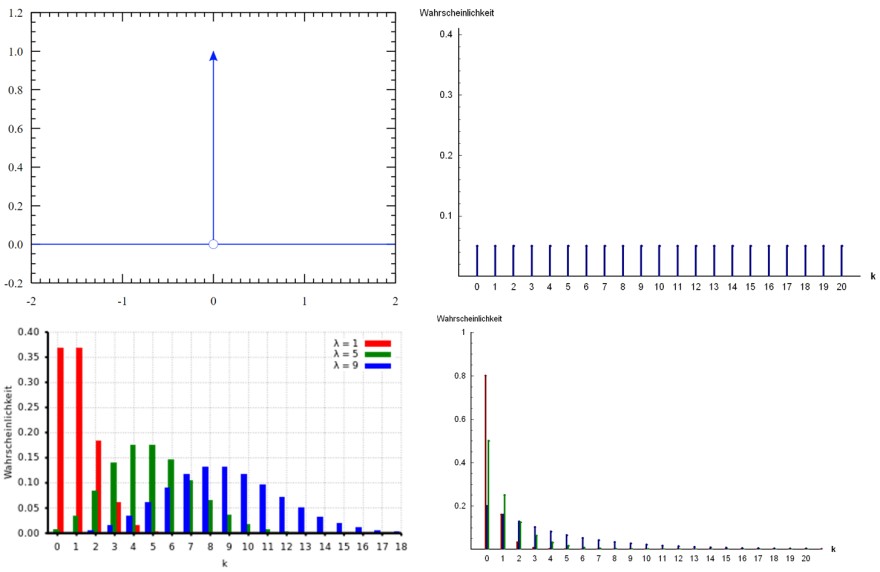

Oben links ist ein Diracmaß, hier ist die ganze Masse auf \(0\). Daneben eine Gleichverteilung, hier kriegt jeder Punkt dieselbe Masse. Unten links sind drei Poisson-Verteilung für verschiedene Parameter und daneben eine geometrische Verteilung.

\(p\) ist nun definiert als$$p(x)=\begin{cases}P(X=x_i) \text{ für } x=x_i \in \{x_1,..,x_k,...\} \\ 0 , \quad \quad \quad \quad \text{ sonst.}\end{cases}$$ ordnet also jedem Punkt seine Masse zu.