Extremstellen von f bestimmen

Question

Aufgabe:Bestimmen sie die Extremstellen von f

Problem/Ansatz:

a) f(x)= e⁴^x-4x

b) f(x)= x×e^-3x

c) f(x) = (x-2) ×e ^-x

d) f(x)= x²×e^2x+1

Danke für eure Antworten

Comments

a) f '(x) = 0

4*e^(4x) -4 = 0

e^(4x) = 1 = e⁰

4x= 0 , Exponentenvergleich

x= 0

f ''(x) = 16e^(4x)

f ''(0) = 16 -> Minimum

b) f '(x) = e^(-3x) -3x*e^(-3x) = e^(-3x)*(1-3x), Produktregel

f '(x) = 0

1-3x= 0

x = 1/3

f ''(x) = ...

u= 1-3x, u'= -3

v= e^(-3x), v' = -3e^(-3x)

f ''(1/3) = ...

Zur Kontrolle:

https://www.ableitungsrechner.net/

Answer 1

Mit einem notwendigen Kriterium für Extremstellen Kandidaten finden.

Mit einem hinreichenden Kriterium für Extremstellen sicherstellen, dass es sich bei den Kandidaten tatsächlich um Extremstellen handelt.

Answer 2

b)

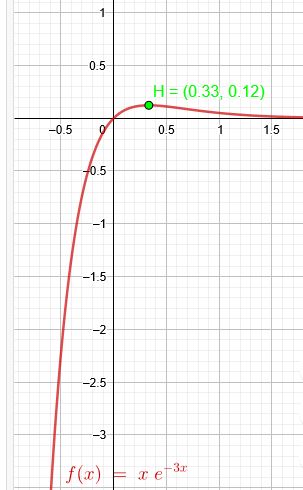
$f(x)= x \cdot e^{-3x}$

$f(x)= \frac{x}{e^{3x}}$

Ableitung mit der Quotientenregel:

$(\frac{Z}{N})'=\frac{Z'N-ZN'}{N^2}$

$f'(x)= \frac{1\cdot e^{3x}-x\cdot e^{3x}\cdot 3}{e^{6x}}=\frac{1-3x}{e^{3x}}$

$\frac{1-3x}{e^{3x}}=0$   mit  $e^{3x}≠0$ 

$x=\frac{1}{3}$       $f(\frac{1}{3})= \frac{\frac{1}{3}}{e^{3\cdot \frac{1}{3}}}=\frac{1}{3e}$

$f''(x)=\frac{(-3)\cdot e^{3x}-(1-3x)\cdot e^{3x}\cdot 3 }{(e^{3x})^2}=\frac{(-3)-(1-3x)\cdot 3 }{e^{3x}}=\frac{-6+9x }{e^{3x}}$

$f''(\frac{1}{3})=\frac{-6+9\cdot \frac{1}{3} }{e^{3\cdot\frac{1}{3}}}=\frac{-3}{e}<0$ Maximum