Geometrieaufgabe: Welches Volumen hat der Dachstuhl und wie groß ist die Dachfläche?

Question

Aufgabe: Welches Volumen hat der Dachstuhl und wie groß ist die Dachfläche?

Problem/Ansatz: Ein Haus besitzt einen Dachstuhl, dessen Giebelseite ein gleichseitiges Dreieck bildet. Die Breite des Hauses an der Giebelseite misst b=8,39 m, die Länge beträgt a=13,07 m und die Höhe des Hauses beträgt h=15,14 m. Welches Volumen hat der Dachstuhl und wie groß ist die Dachfläche (ohne die Giebelflächen in m^2 bzw. m^3)?
Rechnen Sie mit den exakten Werten und runden Sie alle Ergebnisse auf zwei Nachkommastellen.

Comments

Berechne die Fläche des Dreiecks. (Dreieckpyramide)

Fläche mal Länge = Volumen

https://www.mathe-lexikon.at/geometrie/geometrische-koerper/pyramide/dreiseitige-pyramide/volumen.html

---

Hallo

aus dem gleichseitigen Dreieck berechne seine Höhe mit Pythagoras, damit die Fläche des Dreiecks und mit der Hauslänge dann das Prisma Dachstuhl. Die Flächen sind einfach die 2 Rechtecke. (Pyramide wie ggT sagt kommt nicht vor.)

Gruß lul

Answer 1

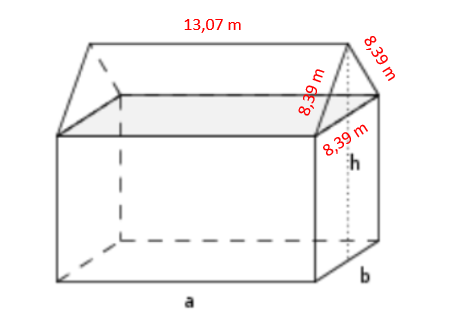
alle Seiten des Dreiecks haben eine Länge von 8,39 m.

Die Dachfläche beträgt also 8,39 m·13,07 m · 2

Die Höhe des Dreiecks rechnen wir mit dem Satz des Pythgoras aus: \(h=\sqrt{8,39^2-(\frac{8,39}{2})^2}=7,27 m\)

damit haben wir eine Dreiecksfläche von 30,48 m². Das ergibt ein Volumen von 398,38 m³. Bitte nachrechnen und bei Unklarheiten nachfragen.

Comments

Vielen Dank für die Antwort!