Wie ihr vielleicht gemerkt habt, teile ich meinen Mathe-Artikel über die Vektoren in drei Tipps auf, da der Platz dafür leider nicht ausreicht. Im ersten Teil haben wir uns angeschaut, was ein Vektor ist. Hier lernen wir nun Ebenen und die Gerade im Raum kennen. Im dritten und letzten Teil werde ich dann ein Beispiel geben.
c) Ebenen (allerdings nicht vollständig)
Eine Ebene im Koordinatensystem wird durch drei Vektoren "gebildet":
- den Stützvektor
- zwei Spannvektoren
Der Stützvektor stützt die Ebene, die Spannvektoren spannen die Ebene auf. Es gibt drei möglichkeiten, Ebenen anzugeben.
a) Parameterform
Bei der Parameterform benötigt man die drei oben genannten Vektoren. Dabei nenne ich den Stützvektor mal V(p), die Spannvektoren nenne ich V(u) und V(v). Dann ergibt sich folgende Gleichung:
$$ E: \vec{ x }= \vec{ p } +r*\vec{ u }+s*\vec{ v } $$
b) Normalenform
Um von der Parameterform in die Normalenform zu kommen, benötigen wir unsere zwei Spannvektoren. Wir müssen jetzt nämlich den Normalenvektor berechnen - diesen erhält man durch das Kreuzprodukt der Stützvektoren. Nun fehlt uns noch ein Vektor p. Das ist irgendein beliebiger Punkt auf der Ebene. Am besten nehmen wir hier den Stützvektor. Dann erhält man folgende Form:
$$ E: \vec{ n }*( \vec{ x } -\vec{ p }) = 0 $$.
Das können wir jetzt umstellen:
$$ E: \vec{ n }*\vec{ x } = \vec{ n }*\vec{ p } $$
c) Koordinatenform
Um nun von der Normalenform in die Koordinatenform zu kommen, multiplizieren wir die erste Gleichung der Normalenform einfach aus. Der Vektor x hat die Koordinaten x1, x2, x2 bzw. x, y und z. Das ist hier wichtig!
d) Die Gerade im Raum
Ihr kennt ja bereits eine Gerade im zweidimensionalen Koordinatensystem. Eigentlich habt ihr dort mit der Bestimmung des Steigungsdreiecks schon irgendwie mit Vektoren im zweidimensionalen Raum gearbeitet. Denn um von Punkt A nach Punkt B zu kommen, kann man entweder den direkten Weg wählen oder über das Steigungsdreieck gehen.
Nun aber wieder in das R³.
Eine Gerade wird durch einen Stützvektor und einen Richtungsvektor gebildet:
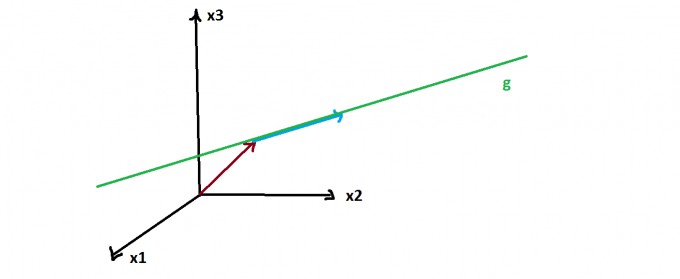
Dabei stützt der Richtungsvektor die Gerade und der Richtungsvektor gibt die Richtung an. Die allgemeine Form einer Geraden ist also:
$$ g: \vec{ x } = \vec{ p } +t* \vec{ u } $$
Dabei ist p der Stützvektor, u der Richtungsvektor und t eine Variable.
Kommen wir nun zu der Lage zweier Geraden. Geraden können wie folgt sein:
a) parallel
b) identisch
c) sich schneidend
d) windschief
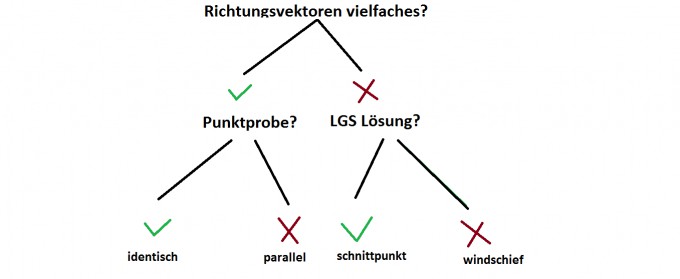
Um zwei Geraden auf ihre Lage zueinander zu überprüfen, musst du immer zunächst schauen, ob der Richtungsvektor Vielfaches deines Stützvektors ist. Trifft dies zu, machst du eine sogenannte Punktprobe. Dazu setzt du einfach den Richtungsvektor der einen Geraden in die andere Gerade ein, indem du das quasi "aufsplittest", alles nach t umformst und jeweils schaust, ob jedes t das selbe ist. Trifft das erste Kriterium jedoch nicht zu, musst du ein LGS aufstellen. Dazu splittest du das quasi wieder auf:
\( g: \vec{x}=\left(\begin{array}{c}{7} \\ {-2} \\ {2}\end{array}\right)+t \cdot\left(\begin{array}{l}{2} \\ {3} \\ {1}\end{array}\right) \)
\( h: x=\left(\begin{array}{c}{4} \\ {-6} \\ {-1}\end{array}\right)+r\left(\begin{array}{l}{1} \\ {1} \\ {2}\end{array}\right) \)
→ LGS aufstellen:
\( 7+2 t=4+r \)
\( -2+3 t=-6+r \)
\( 2+t=-1+2 r \)
Jetzt kannst du nach folgenden Kriterien die Lage deiner Geraden bestimmen:
Hier geht es weiter mit Teil 3.