1) Ermittle eine Gleichung eines Kreises, der durch die Punkte A(6/6) und B(0/-4) geht und dessen Mittelpunkt auf der Geraden g: x = -2 liegt!
Wenn ein Kreis durch die Punkte A und B geht muss der Mittelpunkt sich auf der Mittelsenkrechten zwischen A und B befinden.
Mittelpunkt zwischen A und B:
M_AB = 1/2 * (A + B) = [3, 1]
Steigung zwischen A und B
m_AB = (y1 - y2) / (x1 - x2) = (6 - (-4)) / (6 - 0) = 10/6 = 5/3
Mittelsenkrechte:
h(x) = m * (x - Px) + Py = -3/5 * (x - 3) + 1 = 2.8 - 0.6·x
Schnittpunkt von g und h. Da brauche ich nur x = -2 in h einsetzen
h(-2) = 4
Der Kreismittelpunkt ist damit M(-2, 4).
Der Radius ist der Abstand von Punkt A oder B zum Kreismittelpunkt
r = √((6 - (-2))^2 + (6 - 4)^2) = √68
Also lautet die Kreisgleichung
K: (x + 2)^2 + (y - 4)^2 = 68
2) Stelle Gleichungen der Tangenten an diesen Kreis in den Punkten A und B auf!
Die Tangente bei A geht durch den Punkt A und hat eine Steigung senkrecht zur Geraden durch den Kreismittelpunkt und A.
m_MA = (6 - 4) / (6 - (-2)) = 1/4
Damit lautet die Tangente in A
ta(x) = m * (x - Px) + Py = -4 * (x - 6) + 6
Genauso wird die Tangente in B gemacht.
m_MB = (-4 - 4) / (0 - (-2)) = -4
tb(x) = m * (x - Px) + Py = 1/4 * (x - 0) - 4
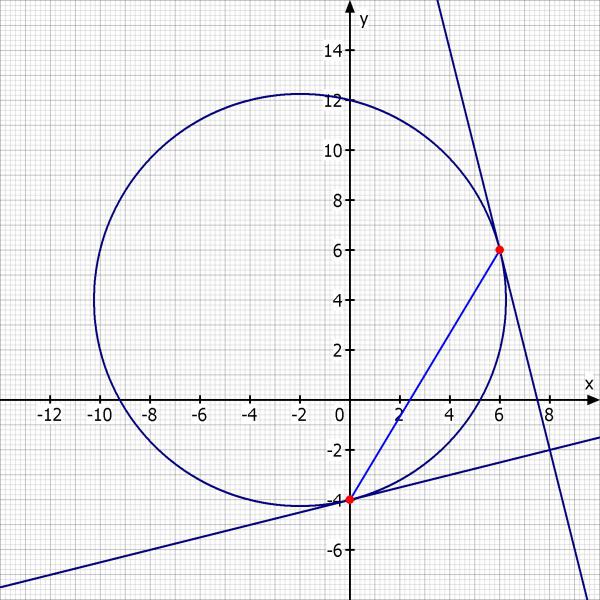
Skizze: