Teil 2: https://www.mathelounge.de/529253/artikel-regression-berechnung-regressionskoeffizienten
1. Einführung
Mit der Methode der kleinsten Quadrate kann man zu einer gegebenen Menge von Punkten eine Funktion finden, die möglichst nahe an den Punkten verläuft. Wir werden in diesem Artikel eine allgemeine Formel zur Berechnung einer linearen Ausgleichsfunktion $$y=a_0+a_1x$$ für endlich viele Messwerte herleiten, welche in ein Java-Programm gegossen und für diverse Probleme, bei denen Ausgleichsrechnungen eine Rolle spielen (physikalische Experimente, statistische Untersuchungen, ...), genutzt werden kann.
2. Datenpaare
Für unseren Algorithmus definieren wir einen neuen Datentyp „Data“, der Datenpaare repräsentiert. Bei Datenpaaren handelt es sich um \(2-\)Tupel (geordnete Paare) der Form \((x,y)\) mit \(x,y\in\mathbb{R}\). \(x\) und \(y\) werden als private, unveränderliche Objektvariablen vom Typ double gespeichert und im Konstruktor zugewiesen. Mit zwei Akzessormethoden (Getter) können diese Werte aus einem Data-Objekt gelesen werden. Eine mögliche Implementierung sieht wie folgt aus:
public class Data {
// x-Wert
private final double x;
// y-Wert
private final double y;
// Konstruktor
public Data(final double x, final double y){
this.x = x;
this.y = y;
}
// Getter für den x-Wert
public double get_x(){
return this.x;
}
// Getter für den y-Wert
public double get_y(){
return this.y;
}
}
Gegeben seien \(n\) Datenpaare \((x_1,y_1),(x_2,y_2), ..., (x_n,y_n)\), die linear durch $$y=a_0+a_1x$$ mit \(a_0,a_1\in\mathbb{R}\) approximiert werden sollen. Gesucht ist die Lösung des linearen Gleichungssystems \(A^TAx=A^Tb\). Dabei ist \(x= \left( \begin{matrix} a_0&a_1 \end{matrix} \right)^T \), \(b=\left( \begin{matrix} y_1&y_2&...&y_n \end{matrix} \right)^T \) und \(A\in\mathbb{R}^{n\times 2}\) eine Matrix, die folgende Gestalt besitzt: $$ A=\left( \begin{matrix} 1&x_1\\ 1&x_2\\ \vdots&\vdots\\ 1&x_n \end{matrix} \right) $$ Setzen wir \(A, A^T, x \) und \(b\) in \(A^TAx=A^Tb\), so erhalten wir: $$ \underbrace{\left( \begin{matrix} 1&1&...&1\\ x_1&x_2&...&x_n \end{matrix} \right)\cdot \left( \begin{matrix} 1&x_1\\ 1&x_2\\ \vdots&\vdots\\ 1&x_n \end{matrix} \right) }_{A^TA}\cdot \underbrace{\left( \begin{matrix} a_0\\ a_1 \end{matrix} \right)}_{x} = \underbrace{\left( \begin{matrix} 1&1&...&1\\ x_1&x_2&...&x_n\\ \end{matrix} \right)\cdot \left( \begin{matrix} y_1\\ y_2\\ \vdots\\ y_n \end{matrix} \right)}_{A^Tb} $$ Wir berechnen \(A^TA\) und erhalten: \( A^TA=\left( \begin{matrix} 1&1&...&1\\ x_1&x_2&...&x_n \end{matrix} \right)\cdot \left( \begin{matrix} 1&x_1\\ 1&x_2\\ \vdots&\vdots\\ 1&x_n \end{matrix} \right) = \left( \begin{matrix} n & x_1+x_2+...+x_n\\ x_1+x_2+...+x_n&x^2_1+x^2_2+...+x^2_n \end{matrix} \right)\\ =\left( \begin{matrix} n & \sum\limits_{k=1}^{n}{x_k}\\ \sum\limits_{k=1}^{n}{x_k}&\sum\limits_{k=1}^{n}{x^2_k} \end{matrix} \right) \) Die Inverse \(\left(A^TA\right)^{-1}\)
der Matrix \(A^TA\), die zur Lösung des linearen Gleichungssystems genutzt wird, berechnen wir wie folgt. Sei \(\varphi := \det(A^TA)^{-1}\) gegeben durch $$ \varphi := \dfrac{1}{\det\left(A^TA\right)} = \dfrac{1}{n\cdot \sum\limits_{k=1}^{n}{x^2_k} - \left(\sum\limits_{k=1}^{n}{x_k}\right)^2} $$ Dann besitzt \(\left(A^TA\right)^{-1}\) folgende Gestalt: $$ \left(A^TA\right)^{-1}= \varphi\cdot \left( \begin{matrix} \sum\limits_{k=1}^{n}{x^2_k} & -\sum\limits_{k=1}^{n}{x_k}\\ -\sum\limits_{k=1}^{n}{x_k}&n \end{matrix} \right) $$ Nun berechnen wir \(A^Tb\) und erhalten: $$ A^Tb=\left( \begin{matrix} 1&1&...&1\\ x_1&x_2&...&x_n\\ \end{matrix} \right)\cdot \left( \begin{matrix} y_1\\ y_2\\ \vdots\\ y_n \end{matrix} \right)= \left( \begin{matrix} y_1+y_2+...+y_n\\ x_1\cdot y_1+x_2\cdot y_2+...+x_n\cdot y_n\\ \end{matrix} \right) = \left( \begin{matrix} \sum\limits_{k=1}^{n}{y_k}\\ \sum\limits_{k=1}^{n}{x_k\cdot y_k} \end{matrix} \right) $$ Den Lösungsvektor \(x= \left(\begin{matrix} a_0\\ a_1 \end{matrix}\right) \) erhalten wir durch beidseitige Multiplikation der Inversen von \(A^TA\), denn $$\underbrace{\left(A^TA\right)^{-1}\cdot A^TA}_{=I_n} \cdot x = \left(A^TA\right)^{-1}A^Tb\Longleftrightarrow x=\left(A^TA\right)^{-1}A^Tb$$ Der Lösungsvektor ist also: \(x= \left(\begin{matrix} a_0\\ a_1 \end{matrix}\right)= \varphi\cdot \left( \begin{matrix} \sum\limits_{k=1}^{n}{x^2_k} & -\sum\limits_{k=1}^{n}{x_k}\\ -\sum\limits_{k=1}^{n}{x_k}&n \end{matrix} \right)\cdot \left( \begin{matrix} \sum\limits_{k=1}^{n}{y_k}\\ \sum\limits_{k=1}^{n}{x_k\cdot y_k} \end{matrix} \right) \\\\\\ =\varphi \cdot \left( \begin{matrix} \left(\sum\limits_{k=1}^{n}{y_k}\right)\cdot \left(\sum\limits_{k=1}^{n}{x^2_k}\right)-\left(\sum\limits_{k=1}^{n}{x_k}\right)\cdot \left(\sum\limits_{k=1}^{n}{x_k\cdot y_k}\right)\\ n\cdot \left(\sum\limits_{k=1}^{n}{x_k\cdot y_k}\right)-\left(\sum\limits_{k=1}^{n}{x_k}\right)\cdot \left(\sum\limits_{k=1}^{n}{y_k}\right) \end{matrix} \right) \)
Die Regressionskoeffizienten \(a_0\) und \(a_1\) der linearen Ausgleichsgerade $$ y=a_0+a_1\cdot x $$ können demnach direkt durch
- \(a_0=\varphi\cdot \left(\left(\sum\limits_{k=1}^{n}{y_k}\right)\cdot \left(\sum\limits_{k=1}^{n}{x^2_k}\right)-\left(\sum\limits_{k=1}^{n}{x_k}\right)\cdot\left(\sum\limits_{k=1}^{n}{x_k\cdot y_k}\right)\right)\)
- \(a_1=\varphi\cdot\left(n\cdot \left(\sum\limits_{k=1}^{n}{x_k\cdot y_k}\right)-\left(\sum\limits_{k=1}^{n}{x_k}\right)\cdot \left(\sum\limits_{k=1}^{n}{y_k}\right)\right)\)
berechnet werden. Diese Funktion bietet die bestmöglichste Approximation an die gegebenen Messwerte mit dem kleinsten Betrag für den Fehlervektor \(e\) nach der Methode der kleinsten Quadrate.
3. Implementierung
Wir stellen in einer beliebigen Klasse eine statische Utility-Funktion mit dem Namen „regression“, die als Argument eine Liste mit Data-Objekten erhält und die lineare Regression gemäß der des im vorangegangenen Abschnitt entwickelten Algorithmus vornimmt. Die Ergebnisparameter \(a_0\) und \(a_1\) werden in einem Array vom Typ double gespeichert und zurückgegeben.
public static double[] regression(final List<Data> data){
final double[] result = new double[2];
// Definition der Variablen für den Algorithmus
double phi = 0;
double sum_of_x_squared = 0;
double sum_of_x = 0;
double sum_of_y = 0;
double sum_of_x_times_y = 0;
double a_0 = 0;
double a_1 = 0;
final int m = data.size();
// Berechnen der Summen
for(final Data data_point : data){
sum_of_x_squared += Math.pow(data_point.get_x(), 2);
sum_of_x += data_point.get_x();
sum_of_y += data_point.get_y();
sum_of_x_times_y += (data_point.get_x() * data_point.get_y());
}
phi = 1.0/(m * sum_of_x_squared - Math.pow(sum_of_x, 2));
// Berechnen der Regressionskoeffizienten
a_0 = phi * (sum_of_y * sum_of_x_squared - sum_of_x * sum_of_x_times_y);
a_1 = phi * (m * sum_of_x_times_y - sum_of_x * sum_of_y);
// Ausgabe
System.out.println(a_0 + (a_1 == 0 ? "" : (a_1 > 0 ? "+" : ""))+a_1+"*x");
// Abspeichern der Ergebnisse
result[0] = a_0;
result[1] = a_1;
return result;
}
4. Beispiel für die schrittweise Ermittlung der Regressionsgeraden
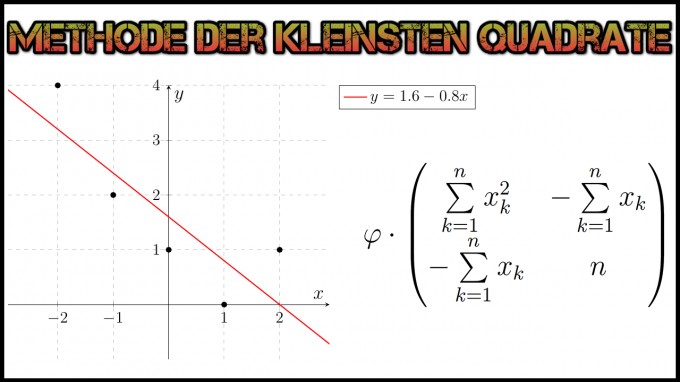
Gegeben seien die Messwerte \(\{(x,y)\mid x,y\in\mathbb{R}\} :=\left\{(-2,4),(-1,2),(0,1),(1,0),(2,1)\right\}\). Wir suchen die lineare Ausgleichsgerade: \(y=a_0\cdot x+a_1\) mit \(a_0,a_1\in\mathbb{R}\) (die Form der Ausgleichsgeraden kann je nach Aufgabenstellung abweichen; beziehen Sie dies in Ihre Modellierung ein!). Mit den gegebenen Messwerten besitzt \(A\) die Form $$A=\left( \begin{matrix} -2&1\\ -1&1\\ 0&1\\ 1&1\\ 2&1\\ \end{matrix} \right)\text{ bzw. }A^T=\left( \begin{matrix} -2&-1&0&1&2\\ 1&1&1&1&1 \end{matrix} \right)$$ Zu lösen ist folgendes lineare Gleichungssystem: $$\underbrace{A^T\cdot \left( \begin{matrix} -2&1\\ -1&1\\ 0&1\\ 1&1\\ 2&1\\ \end{matrix} \right)}_{A^T A}\cdot \left(\begin{matrix} a_0\\ a_1 \end{matrix}\right) = \underbrace{A^T \cdot\left(\begin{matrix} 4\\ 2\\ 1\\ 0\\ 1 \end{matrix}\right) }_{A^T b}$$ Wir berechnen \(A^TA\): $$A^TA=\left( \begin{matrix} -2&-1&0&1&2\\ 1&1&1&1&1 \end{matrix} \right)^T\cdot \left( \begin{matrix} -2&1\\ -1&1\\ 0&1\\ 1&1\\ 2&1\\ \end{matrix} \right)= \left(\begin{matrix} 10&0\\ 0&5 \end{matrix} \right) $$ Anschließend ermitteln wir \(A^T b\): $$ \left( \begin{matrix} -2&-1&0&1&2\\ 1&1&1&1&1 \end{matrix} \right) \cdot\left(\begin{matrix} 4\\ 2\\ 1\\ 0\\ 1 \end{matrix}\right)= \left(\begin{matrix} -8\\ 8 \end{matrix}\right) $$ Wir lösen also folgendes lineare Gleichungssystem: $$ \left(\begin{matrix} 10&0\\ 0&5 \end{matrix} \right) \cdot \left(\begin{matrix} a_0\\ a_1 \end{matrix}\right) = \left(\begin{matrix} -8\\ 8 \end{matrix}\right) $$ Die Lösung kann mittels der Inversen oder dem Gauß-Jordan-Verfahren ermittelt werden. Man erhält schlussendlich: $$\left(\begin{matrix} a_0\\ a_1 \end{matrix}\right)= \left(\begin{matrix} -0.8\\ 1.6 \end{matrix}\right) $$ Die Gleichung der Ausgleichsgerade lautet also $$y=-0.8x+1.6=1.6-0.8x$$
Im nächsten Teil werden wir dieses Ergebnis mit unserem Programm verifizieren.