Arithmetische Reihe als Integralrechnung

Question

aufgrund der Fragestellung in

https://www.mathelounge.de/534547/eine-brunnenbaufirma-stellt-folgendes-angebot#c534734

kamen mir einige Gedanken wie man die Integralrechnung
bei arithmetischen Reihen nutzen kann.

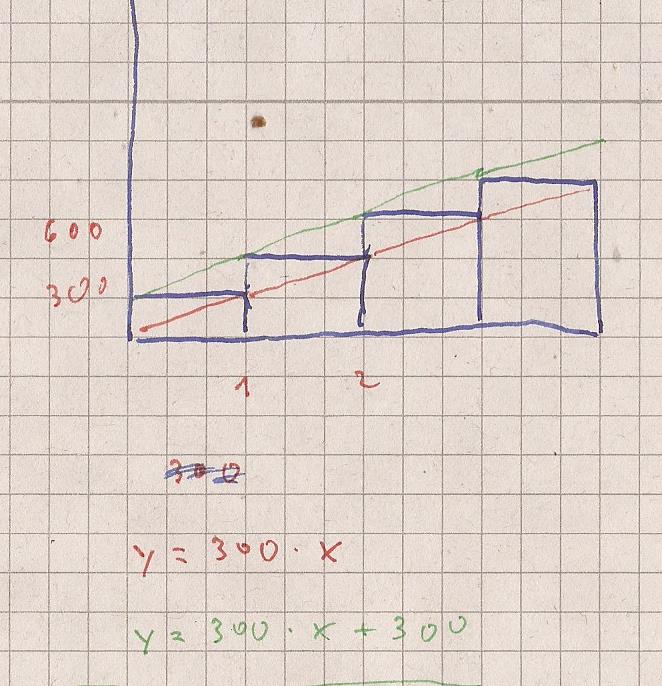
Die Skizze zeigt den treppenförmigen Verlauf ( Balkendiagramm )
einer arithmetischen Reihe mit

Anfangsglied 300
Endglied 1200
Anzahl 4 ( Balken )

( Einschub : für den der es noch nicht weiß.
1. plus 4. Balken : 300 + 1200 = 1500
2. plus 3. Balken : 600 + 900 = 1500
daraus abgeleitet
)
Summe = ( Anfang + Ende ) * Anzahl / 2
Summe = ( 300 + 1200 ) * 4 / 2 = 3000

Die Aufgabe kann auch mit Integralrechnung
gelöst werden.
Rote Gerade : y = 300 * x ( Untersumme )
Grüne Gerade : y = 300 * x + Anfang  ( Obersumme )
Grüne Gerade : y = 300 * x + 300  ( Obersumme )

Dazwischen
y = 300 * x + Anfang / 2

Fläche
∫ 300 * x + Anfang / 2 dx zwischen 0 und 4
∫ 300 * x + 300 / 2 dx zwischen 0 und 4

[ 300 * x^2 / 2 + 150 * x ] zwischen 0 und 4
2400 + 600 = 3000

Die Ergebnisse Arithmetische Reihe / Integralrechnung
stimmen überein.

Die Integrallösung ist auch für Größeres bzw
für Zwischenwerte geeignet ( z.B. x = 4.3 ).

Comments

Du hast die Begriffe "Untersumme" und "Obersumme" verwechselt.

---

Eine Variation des Ansatzes wäre:

int(300*x+150,x=0..4) = 3000 

Dabei ist der Integrand eine Gerade zwische der roten und der grünen Geraden.

---

Hallo

 das Integralrechnung zu nennen ist etwa übertrieben, die fläche eines dreiecks kann man auch direkt ausrechnen und sehen, dass bei der mittleren Geraden die Fläche der Rechtecke gleich der Fläche des Dreiecks ist auch.

Gruß lul

---

Hallo Georg,

Die Darstellung mit der grünen und roten Line hilft einem sehr, die Thematik besser zu verstehen. In­tu­i­tiv wäre darauf niemals gekommen die Integralrechnung anzuwenden. Danke für den etwas anderen Rechenweg! Finde ich eine gute Alternative zur arithmetischen Reihe.

Ich frage mich, wieso das noch kein Wissensartikel ist?

---

Generell kann es oft ungemein hilfreich
sein sich ein Bild zu zeichnen.

---

Noch mal: Integralrechnung auf etwas anzuwenden, das man einem S von ca 10 Jahren leicht erklären kann, ist wirklich nicht nützlich und sicher keine Wissenserweiterung. So wenig, wie zu zeigen, dass man die Fläche eines Dreiecks oder Rechtecks mit Integralrechnung bestimmen kann.

Gruß lul

Answer 1

Ich muss lul völlig recht geben.

Mit der Integralrechnung kann man vieles machen. Man kann damit sogar Flächeninhalte von Rechtecken ermitteln. Aber das ist wie mit Kanonen auf Spatzen zu schießen. Das macht man nicht. Meine 10 Jährige Nichte lernt gerade Flächeninhalte von Rechtecken zu berechnen. Wann lernt man noch die Integralrechnung?

Answer 2

Diese Art von Integralrechnung könntest du sehr früh einführen.

Oft wird später bei der Einführung der Integralrechnung die neue Methode benutzt um (vor der mündlichen Maturprüfung) altbekannte Formeln zu festigen und Zusammenhänge sichtbar zu machen.