Geometrie: Gesucht ist ein Beweis im Dreieck mit Inkreis und Umkreis

Question

Hallo Freunde der Geometrie,

bei der Suche nach einer Antwort auf diese Frage, bin ich auf einige interessante Zusammenhänge gestoßen. Eine dieser frappierend einfachen Abhängigkeiten ist diese hier:

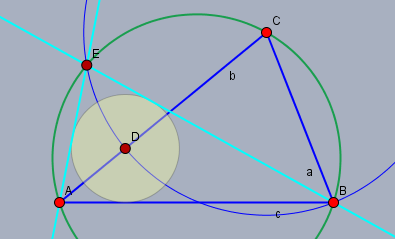
Gegeben ist ein stumpf¹⁾winkliges Dreieck \(\triangle ABC\), mit \(a \lt b\). Der Kreis (blau) um \(C\) mit Radius \(a=|BC|\) schneidet die Seite \(AC\) in \(D\) und den Umkreis (grün) von \(\triangle ABC\) außer in\(B\) noch in \(E\).

Beweise, dass \(D\) der Inkreismittelpunkt von \(\triangle ABE\) ist.

Fröhliches Knobeln ;-)

Bem.: zu 1.) gemeint war spitzwinklig, was aber auch nicht nötig ist.

Comments

Zitat WS :   die Aufgabe ist nicht schwer ...

Es ist  α = β  (Peripheriewinkel-Satz)
→ erste Winkelhalbierende gesichert

ε  =  ζ - β  (Außenwinkelsatz)
    =  ζ - γ  (Peripheriewinkel-Satz)
    =  (δ+γ) - γ  (Satz vom gleichsch. Dreieck)
    =  δ
→ zweite Winkelhalbierende gesichert

---

Hallo WS,

die Voraussetzung "stumpfwinkliges Dreieck" scheint mir unnötig zu sein, wie deine eigene Abbildung mit einem spitzwinkligen Dreieck zeigt.

---

die Aufgabe ist nicht schwer ...

@hj: ganz meine Meinung, aber schwer genug, so dass außer Dir niemand geantwortet hat ;-)

---

die Voraussetzung "stumpfwinkliges Dreieck" scheint mir unnötig zu sein

stimmt: gemeint war natürlich spitzwinklig, aber auch das ist unnötig. Wie das folgende Applet zeigt:

https://jsfiddle.net/WernerSalomon/5soakfq2/1/