Rotationen im Geoknecht3D (Teil 1)
Der Geoknecht3D ist in meinen Augen ein gelungenes und absolut hilfreiches Tool. Man kann sehr schnell Punkte, Geraden und Vektoren usw. darstellen. Und auch einfache Körper wie Quader und Zylinder. Wobei man aus dem Zylinder auch Kegel und quadratische Pyramiden machen kann.
Die Körper können auch gedreht werden. Nur diese Funktion ist alles andere als 'einfach'! Man muss dazu sagen: Rotationen sind per se nicht einfach - aber zunächst einmal sei die Frage zu klären:
Was macht die Rotation genau?
In der Hilfe heißt es dazu:
Quader, Würfel, Zylinder, Text können in x-y-z-Richtung rotiert werden
Nun ist aber eine Rotation nicht kommutativ und wenn man ein wenig damit experimentiert, so merkt man schnell, dass die Reihenfolge eben nicht x-y-z ist. Sie ist - wenn man sich jeweils auf das lokale System bezieht(!) - y-z-x. Im Folgenden möchte ich das an Hand eines Quaders zeigen.
Der Quader in meinem Beispiel soll an der Position \(p'=(0|\,0|\,0)\) stehen und hat die Seitenlängen 1, 2 und 4. Dafür schreibt man im Geoknecht3D-Script:
quader(0|0|0 1|2|4)
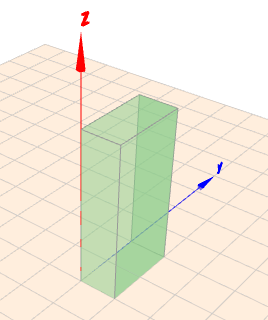
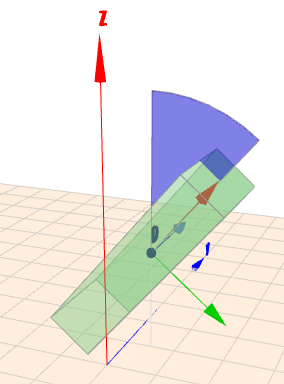
Die Position birgt dann auch noch ein Problem, daher bezeichne ich die Positionskoordinaten in Geoknecht mit \(p'\), aber davon später mehr. Die 1.Rotation geht wie schon oben erwähnt - um die lokale Y-Achse, die durch die Körpermitte des Quaders verläuft. Der Quader soll um \(\beta=40°\) gedreht werden. Demnach ist das Kommando
quader(0|0|0 1|2|4){8c8}[0|40|0]
Die Werte in geschweiften Klammern sorgen nur für die Farbe. Die Drehwinkel stehen hinten in den eckigen Klammern \([\alpha\,|\beta\, |\gamma]\). \(\alpha\) für die Drehung um die X-Achse \(\beta\) für die Drehung um die Y-Achse und \(\gamma\) bleibt dann für den Winkel mit dem um die Z-Achse gedreht werden soll. Geoknecht3D dreht immer um eine Achse durch die Körpermitte! Und so sieht die Rotation um die lokale Y-Achse um \(\beta=40°\) aus:
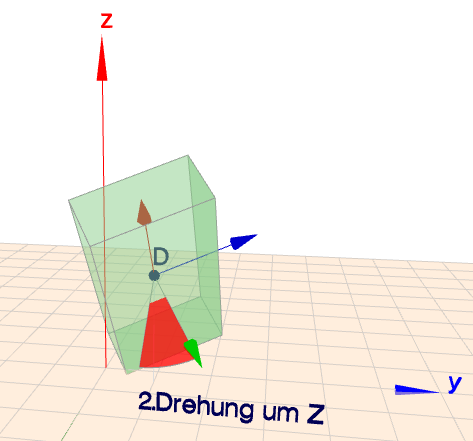
Dann folgt eine Drehung um \(\gamma=30°\) um die lokale Z-Achse des Quaders. Also wird nur der Wert für \(\gamma\) von 0 auf 30 gesetzt:
quader(0|0|0 1|2|4){8c8}[0|40|30]
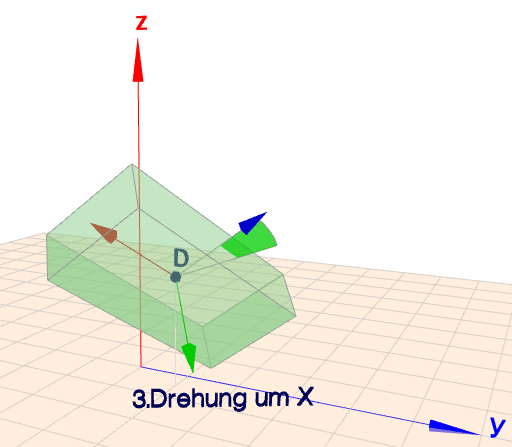
und zum Schluß noch eine Drehung um die lokale X-Achse ... diesmal um \(\alpha=25°\). Das Kommando für Geoknecht3D unterscheidet sich also nur durch die \(25°\) vom vorherigen:
quader(0|0|0 1|2|4){8c8}[25|40|30]
Bildet man die Rotationsmatrizen der drei Drehungen, so sind dies:$$R_y = \begin{pmatrix}\text c_{\beta}& 0& \text s_{\beta}\\ 0& 1& 0\\ -\text s_{\beta}& 0& \text c_{\beta}\end{pmatrix}\\ R_z = \begin{pmatrix}\text c_{\gamma}& -\text s_{\gamma}& 0\\ \text s_{\gamma}& \text c_{\gamma}& 0\\ 0& 0& 1\end{pmatrix} \\R_x = \begin{pmatrix}1& 0& 0\\ 0& \text c_{\alpha}& -\text s_{\alpha}\\ 0& \text s_{\alpha}& \text c_{\alpha}\end{pmatrix}$$Um Platz zu sparen habe ich \(\cos\) und \(\sin\) mit \(\text c\) und \(\text s\) abgekürzt. Und das Produkt dieser Rotationen ist:$$\begin{aligned} R_{yzx} &= R_y \cdot R_z \cdot R_x\\&= \begin{pmatrix} \text c_\beta \text c_\gamma & -\text c_\alpha \text c_\beta \text s_\gamma + \text s_\alpha \text s_\beta& \text s_\alpha\text c_\beta \text s_\gamma + \text c_\alpha \text s_\beta\\ \text s_\gamma & \text c_\alpha\text c_\gamma& -\text s_\alpha \text c_\gamma\\ -\text s_\beta \text c_\gamma& \text c_\alpha \text s_\beta \text s_\gamma + \text s_\alpha \text c_\beta& -\text s_\alpha \text s_\beta \text s_\gamma + \text c_\alpha \text c_\beta \end{pmatrix} \end{aligned}$$
Und die Position?
Dem aufmerksamen Leser wird nicht entgangen sein, dass die Position immer noch auf \(p'=(0|\,0|\,0)\) steht. Wenn man sich aber das letzte Bild anschaut, kann man dem Betrachter schwer vermitteln, dass sich dieser Quader immer noch in der Ausgangsposition \(p'=(0|\,0|\,0)\) befindet. Dieser Effekt tritt auf, weil der Punkt, auf den sich die Rotation bezieht, nicht der gleiche ist, wie der auf den sich die Positionsangabe bezieht.
Ich habe den körper-lokalen Ortsvektor des Punktes, um den die Rotation erfolgt, mit \(d\) bezeichnet. Bei Quadern und Würfeln liegt dieser Punkt jeweils in der geometrischen Mitte des Körpers. Da der Punkt, auf den sich die Position des Quaders bzw. Würfels bezieht, an der Ecke mit dem niedrigsten Wert einer Koordinate liegt, hat \(d\) drei Koordinaten \(\ne 0\). Jede Koordinate hat den halben Wert der zugehörigen Kantenlänge des Quaders.
Bei Zylinden geht \(d\) bis zur halben Höhe über dem Mittelpunkt. Das wäre bei 'echten' Zylindern auch die geometrische Mitte, aber im Unterschied zu den Quadern bezieht sich die Position eines Zylinders bereits auf den Mittelpunkt der Grundseite. Somit hat \(d\) hier nur einen Wert in \(Z\), mit dem Wert der halben Höhe des Zylinders. Im Detail ist das jeweilige \(d\)$$d_{\text{Quader}} = \frac 12\begin{pmatrix}l_x\\ l_y\\ l_z\end{pmatrix}, \quad d_{\text{Zylinder}} = \frac 12 \begin{pmatrix}0\\ 0\\ h\end{pmatrix}$$
Um Rotation und Translation (die Verschiebung) nicht unterscheiden zu müssen, wähle ich die Darstellung mit homogenen Koordinaten. Die Transformation von der Positionslage zur Drehlage sei \(D\). $$D = \begin{pmatrix}1& 0& 0& d_x\\ 0& 1& 0& d_y\\ 0& 0& 1& d_z\\ 0& 0& 0& 1\end{pmatrix}$$Diese muss der Rotation voran gestellt werden und nachher wieder invertiert werden.Die eigentliche Positionierung \(P\) des Körpers, die sich aus \(p'\) ergibt, wird ebenfalls vorne angestellt. Ist \(h(R_{yzx})\) die homogene Transformation der Rotation, so ist die vollständige Kinematikkette:$$\begin{aligned} T &= P \cdot D \cdot h(R_{yzx}) \cdot D^{-1} \\&= \begin{pmatrix} R_{yzx} & p'+d - R_{yzx}d \\ \underline 0^T & 1 \end{pmatrix} \end{aligned}$$Unser \(P\) im Beispiel oben ist die Einheitsmatrix. Die Transformation \(D\) ist konkret $$D = \begin{pmatrix}1& 0& 0& 0,5\\ 0& 1& 0& 1\\ 0& 0& 1& 2\\ 0& 0& 0& 1\end{pmatrix}$$Damit ist das \(T\) aus dem Beispiel mit den drei Winkeln \(\alpha=25°\), \(\beta=40°\) und \(\gamma=30°\):$$T=\begin{pmatrix}0,663& -0,075& 0,744& -1,245\\ 0,500& 0,785& -0,366& 0,697\\ -0,557& 0,615& 0,558& 0,546\\ 0& 0& 0& 1\end{pmatrix}$$(auf drei Stellen hinter dem Komma gerundet) das entspricht nach wie vor genau dieser Angabe der Lage des Quaders: quader(0|0|0 1|2|4){8c8}[25|40|30]
Der Positionsanteil von \(T\) ... das ist die vierte Spalte ... ist nun offensichtlich \(\ne p'\). Zur Unterscheidung benenne ich ihn mit \(p\) (ohne \('\)). Und um zu zeigen, dass die bisherigen Berechnungen korrekt sind, stelle ich die Position von \(p\) und die drei Richtungen für die lokale x-, y- und z-Richtung als Vektoren im geoknecht3D dar, die ich hier mit \(n\), \(o\) und \(a\) bezeichne. Man muss lediglich die Zahlenwerte aus \(T\) für einen Punkt bzw. Vektor übernehmen:
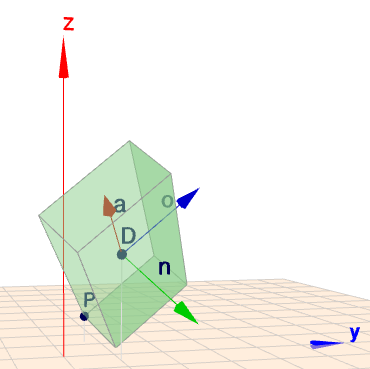
Wie üblich, verbirgt sich hinter jedem Bild ein Link auf die zugehörige Szene in Geoknecht3D.
Und hier geht's zum 2.Teil. Ich musste den Artikel wegen der Größenbegrenzung von 12000 Zeichen teilen.