Hallo, ich soll folgende Rechenregeln beweisen.
Körperaxiome:
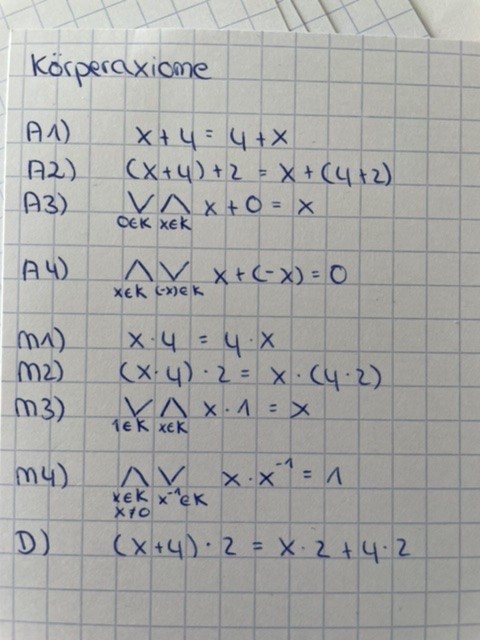
Aufgabe 3: \( \mathrm{K} \) sei ein Körper. Zeigen Sie:
(a) Für alle \( \mathrm{x} \in \mathrm{K} \) gilt: \( \mathrm{x} \cdot 0=0 \).
(b) Für alle \( x \in K \) gilt; \( -(-x)=x \).
(c) Für alle \( x, y \in K \) gilt: \( (-x) \cdot y=-(x \cdot y) \).
(d) Für alle \( x, y \in K \) gilt \( :(-x) \cdot(-y)=x \cdot y \),
(e) Für alle \( x, y \in K \) gilt: \( x \cdot y=0 \Rightarrow x=0 \vee y=0 \).
(f) Für alle \( x, y \in K \) gilt: \( (x+y)^{2}=x^{2}+2 \cdot x \cdot y+y^{2} \).
Problem/Ansatz:
Leider fällt es mir unglaublich schwer, diese Regeln zu beweisen, eventuell könnte ich es nachvollziehen, wenn ich mal gesehen habe wie es funktioniert.
Wäre über jede Hilfe sehr dankbar.
Liebe Grüße