Springer Problem modellieren (Schach)

Question

Aufgabe:

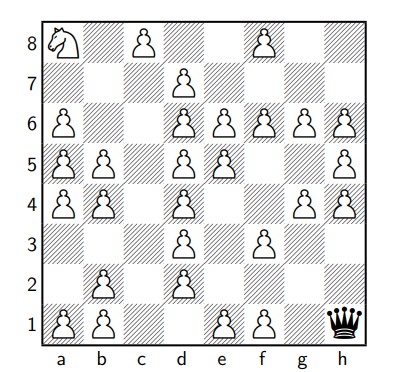
Betrachten Sie das dargestellte Schachbrett. Keine Figur außer dem
weißen Springer darf ziehen. Das Springerproblem besteht darin, zu beweisen,
ob mit dem weißen Springer auf a8 die schwarze Dame auf h1 geschlagen werden kann, wobei einige Felder von weißen Bauern blockiert werden und daher nicht vom Springer betreten werden dürfen. Wenn ja, soll die minimale Anzahl an dafür benötigten Springerzügen angegeben werden.

Problem/Ansatz:

1) Modellieren Sie dieses Problem mit Hilfe eines ungerichteten Graphen und geben Sie eine
Graphentheoretische Formulierung des Springerproblems an.

2)  Verwenden Sie einen geeigneten Algorithmus aus der Vorlesung zur Lösung des unten
dargestellten Springerproblems. Erklären Sie Ihre einzelnen Schritte bei der Anwendung
des Algorithmus.

Comments

einen geeigneten Algorithmus aus der Vorlesung...

Und was für Algorithmen wurden denn vorgelesen?

---

Strong Components Algorithmus und Graph Scanning Algorithmus

---

schau Dir mal meinen Kommentar zu einer ähnlichen Frage an. Vielleicht hilft das weiter.

Answer 1

Naja, mal ganz ohne Computer-Algorithmen:

(1.) es ist leicht, einen Weg in 6 Zügen zu finden (durch Anschauen und ein wenig Probieren); dabei gibt es nicht bloß einen einzigen

(2.) einen Weg in 5 Zügen kann es nicht geben (warum nicht?)

(3.) ein Weg mit weniger als 5 Springer-Zügen kann nicht vom Startfeld a8 zum Zielfeld h1 führen (warum nicht?)

(4.) somit ist 6 die gesuchte minimale Anzahl von Zügen