Nach welcher Zeit wird eine Kerze 3 mal so hoch sein wie die andere?

Question

Aufgabe:

Zwei gleich hohe Kerzen werden gleichzeitig angezündet.
Sie brennen mit konstanter, aber unterschiedlicher Geschwindigkeit.
Eine brennt in 5 Stunden ab, die andere in 3 Stunden.
Nach welcher Zeit wird eine Kerze 3 mal so hoch sein wie die andere?

Problem:

Ich weiß nicht wie ich das ausrechnen soll.

Answer 1

x:   ursprüngliche Kerzenhöhe

t:   Zeit in Stunden

Löse die Gleichung

x - (t/5)x = 3(x - (t/3)x)

nach t auf.

Comments

Das links vom Gleichheitszeichen ist gleich x wenn t = 0 und gleich 0 wenn t = 5. So verhält sich die Länge der Fünfstundenkerze.

Der zweite Faktor rechts vom Gleichheitszeichen ist gleich x wenn t = 0 und gleich 0 wenn t = 3. So verhält sich die Länge der Dreistundenkerze.

Die Fünfstundenkerze brennt langsamer, es ist darum die Fünfstundenkerze welche dreimal so hoch sein muss wie die Dreistundenkerze. Das steht in meiner Gleichung.

Musterlösung: t = 2,5 Stunden.

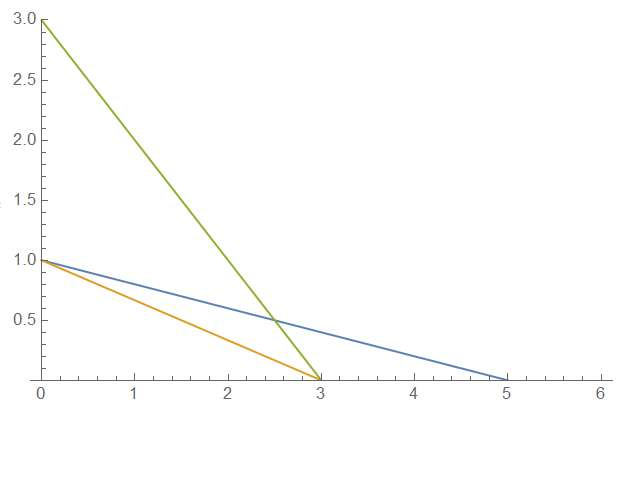
Die Längenmaßeinheit der Kerzenhöhe (Zentimeter, Zoll, sonstwas) ist wurst. Man kann x = 1 KE (Kerzeneinheit) setzen. Die gelbe Linie ist die Dreistundenkerze, die blaue Linie die Fünfstundenkerze. Grün ist eine Hilfslinie die dreimal so hoch ist wie die Dreistundenkerze. Sie schneidet die blaue Linie bei t = 2,5 wo die Fünfstundenkerze dreimal so hoch ist wie die Dreistundenkerze.

Answer 2

Hallo,

$$ 3\ell\cdot(1-\frac{x}{3}) =\ell\cdot(1-\frac{x}{5}) ~~~~~|\div\ell$$

$$3-x=1-\frac{x}{5}~~~~~~~|\cdot5$$

$$15-5x=5-x$$

$$10=4x$$

$$x=2,5$$

:-)