Aufgabe:
Hallo
es geht um folgendes Problem ( letzte Teilaufgabe RC Stromkreis) :
Zeitabhängige Spannungsquelle:
Zum Schluss betrachten wir eine Spannungsquelle, die eine Schwingung erzeugt. Bis zum Zeitpunkt t = 0 ist der Kondensator entladen und die Spannungsquelle erzeugt keine Spannung. Ab t = 0 erzeugt die Spannungsquelle eine Kosinus-Schwingung. Zum Zeitpunkt T > 0 wird die Spannungsquelle wieder ausgeschaltet.
Das heisst
U(t) = Uo cos(ωt) für 0 < t < T
U(t) = 0 sonst
Problem/Ansatz:
Skizzieren Sie anschließend den Verlauf von Q(t) und untersuchen Sie den Grenzfall
1/RC << t für t < t qualitativ.
Die DGL habe ich bereits errechnet ist als Bild hochgeladen. Jedoch bereitet mir das Skizzieren dieses komplizierten Graphen Bauchschmerzen...
LG
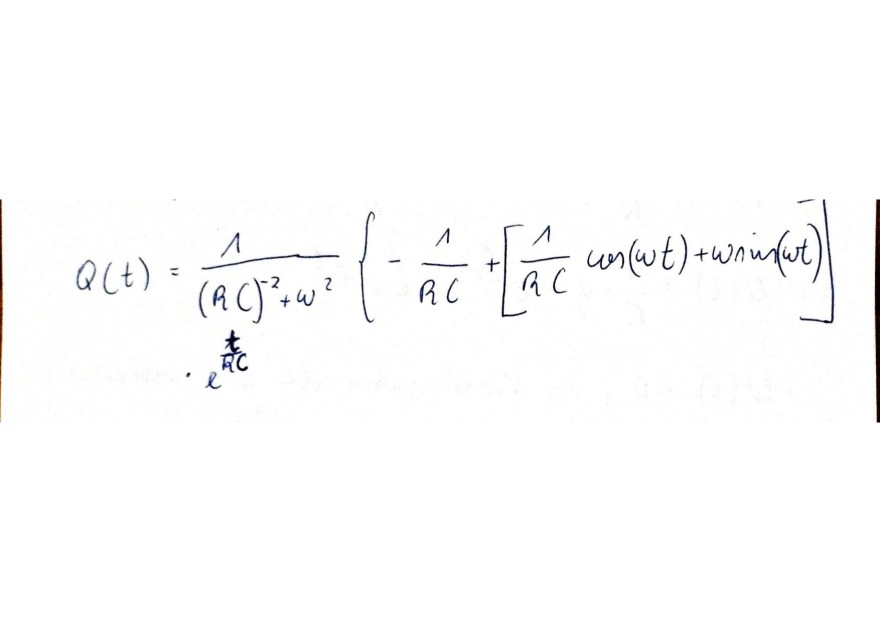
Text erkannt:
\( \begin{array}{l}Q(t)=\frac{1}{(R C)^{-2}+\omega^{2}}\left\{-\frac{1}{R C}+\left[\frac{1}{R C} \cos (\omega t)+\omega \sin (\omega t)\right]\right. \\ \cdot e^{\frac{t}{R C}} \\\end{array} \)