Aufgabe:
Hallo, ich muss die Lagereatktionen ermitteln.
Ich habe von Prof folgenden Ansatz erhalten. Ich verstehe bis zu diesem Punkt alles, aber kann mir jemand nochmal kurz erläutern wie die dritte Gleichung zustande kommt ?
Text erkannt:
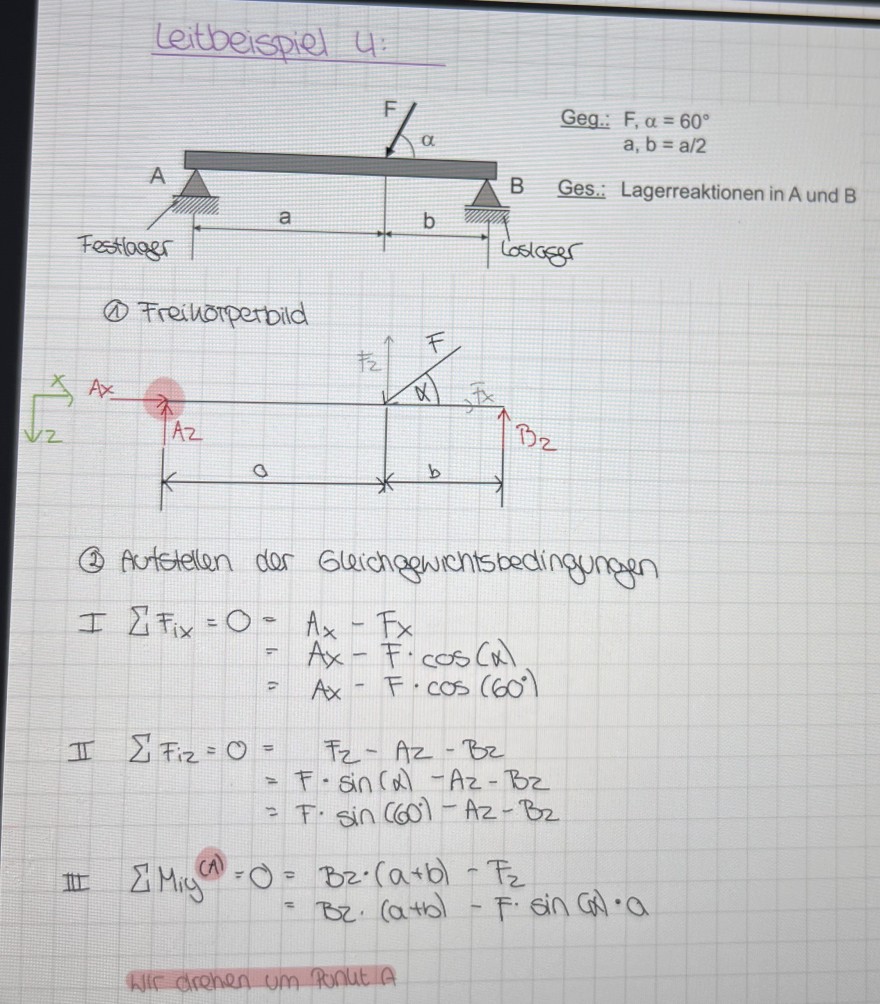
Leitbeispiel 4:
(1) Freinorperbild
(2) Autstellen der Gleichgewichtsbedingungen
\( \begin{aligned} \text { I } \sum F_{i x}=0 & =A_{x}-F_{x} \\ & =A_{x}-F \cdot \cos (\alpha) \\ & =A_{x}-F \cdot \cos \left(60^{\circ}\right) \end{aligned} \)
II
\( \begin{aligned} \Sigma F_{i z}=0 & =F_{z}-A z-B z \\ & =F \cdot \sin (\alpha)-A z-B z \\ & =F \cdot \sin \left(60^{\circ}\right)-A z-B z \end{aligned} \)
III
\( \begin{aligned} \Sigma M_{i} y^{(A)}=0 & =B z \cdot(a+b)-F_{2} \\ & =B z \cdot(a+b)-F \cdot \sin (a) \cdot a \end{aligned} \)
Wlir drehen um Ponut \( A \)
Text erkannt:
Leitbeispiel 4:
(1) Freinorperbild
(1) Autstelen der Gleichgewichtsbedingungen
\( \text { I } \begin{aligned} \Sigma F_{i x}=0 & =A_{x}-F_{x} \\ & =A_{x}-F \cdot \cos (\alpha) \\ & =A_{x}-F \cdot \cos \left(60^{\circ}\right) \end{aligned} \)
II
\( \begin{aligned} \Sigma_{F_{i 2}}=0 & =F_{2}-A_{2}-B_{2} \\ & =F \cdot \sin (\alpha)-A_{2}-B_{2} \\ & =F \cdot \sin \left(60^{\circ}\right)-A_{2}-B_{2} \end{aligned} \)
\( \text { III } \begin{aligned} \Sigma M_{i} y^{(A)}=0 & =B z \cdot(a+b)-F_{2} \\ & =B z \cdot(a+b)-F \cdot \sin (a) \end{aligned} \)