Stabhochsprung Dauer und Latte

Question

Aufgabe:

Die Höhe des Schwerpunktes eines Stabhochspringers kann angenähert durch die Funktion
h(t) = -5t hoch zwei + 9t + 1 erfasst werden (t in Sekunden, h in Metern). Die Matte ist 50 cm hoch.
a) Wie lange dauert der Flug?
b) Der Schwerpunkt muss mindestens 30 cm über die Latte geliftet werden, um deren Reißen zu vermeiden. Wie geht der beschriebene Sprung aus, wenn die Latte in 5 m Höhe liegt?
c) Mit welcher Geschwindigkeit prallt der Springer auf die Matte?
d) Wie lange befindet sich der Schwerpunkt des Springers über der Latte?

Problem/Ansatz:

Mein Ansatz für a) wäre die Funktionsgleichung gleich 0 zu setzen, bei c) muss es irgendwas mit der ersten Ableitung zu tun haben. Für die restlichen Aufgaben habe ich gar keinen Ansatz? Könnte mir jemand helfen bzw. mir eine Denkanstoß geben? Danke!

Answer 1

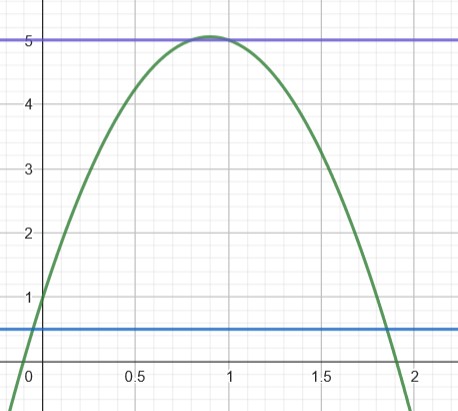
so sieht der Verlauf aus. Die untere Linie entspricht der Mattenhöhe.

a) du musst den Schnittpunkt errechnen, die quadratische Funktion muss als nicht =0 gesetzt werden, sondern =0,5

b) der höchste Punkt liegt bei 5,05 m, das reicht nicht

c) der Springer fällt aus 5,05 m auf 0,5 m; die Geschwindigkeit berechnest du mit \(v=\sqrt{2 \cdot g\cdot h}\)

d) ähnlich wie bei a), rechne die Schnittpunkte mit der oberen Geraden aus und du bekommst die Zeitdifferenz

zeig 'mal deine Ergebnisse und melde dich bei Unklarheiten.

Comments

Vielen Dank für Ihre ausführliche und liebe Antwort!

Bei a) habe ich nun t≈1,8

b) Habe ich mithilfe der 1. Ableitung gelöst und habe den Hochpunkt (0,9|5,05), demnach ist der Abstand von 30cm über der Latte nicht gegeben.

c) Auch mithilfe der ersten Ableitung (Mein Lehrer bestand darauf): Ich habe für t=1,85 eingesetzt und dann kam eine Geschwindigkeit von ca. (-)9,5 m/s heraus.

d) Ich habe die Gerade mit der Parabelgleichung gleichgesetzt, p-q-Formel verwendet und dann t1-t2 gerechnet, wobei dann eine Zeit von 0,2 Sekunden die Lösung war.

---

prima, dass du selbst weitergearbeitet und gerechnet hast. Einige Anmerkungen:

für a) würde ich es etwas genauer mit t≈1,854 s ansetzen.

b) sehr schön

c) auf die Geschwindigkeit komme ich auch, jetzt brauche ich deine Hilfe, wie kommt man von 1,85 s auf (-)9,5 m/s?

d) perfekt!