Aufgabe: Integral bestimmen
Problem/Ansatz: Kann mir jemand vielleicht erklären wie man hier auf die y-1 kommt verstehe irgendwie nicht woher die -1 auftaucht. 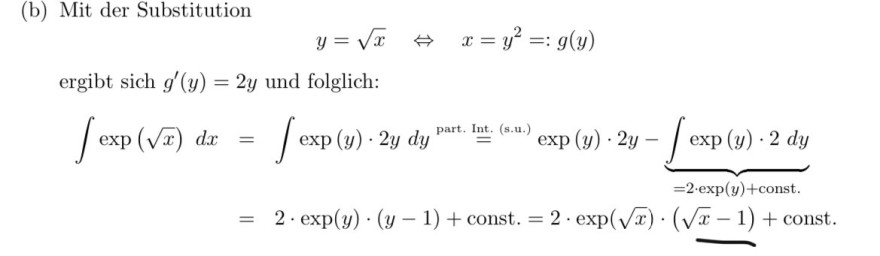
Text erkannt:
(b) Mit der Substitution
\( y=\sqrt{x} \quad \Leftrightarrow \quad x=y^{2}=: g(y) \)
ergibt sich \( g^{\prime}(y)=2 y \) und folglich:
\( \begin{aligned} \int \exp (\sqrt{x}) d x & =\int \exp (y) \cdot 2 y d y \stackrel{\text { part. Int. (s.u.) }}{=} \exp (y) \cdot 2 y-\underbrace{\int \exp (y) \cdot 2 d y}_{=2 \cdot \exp (y)+\text { const. }} \\ & =2 \cdot \exp (y) \cdot(y-1)+\text { const. }=2 \cdot \exp (\sqrt{x}) \cdot(\sqrt{x}-1)+\text { const. } \end{aligned} \)