Fakultät und Quotientenkriterium

Question

Aufgabe:

Hallo zusammen,

ist mein Ansatz und die Lösung der Aufgabe korrekt? Zu zeigen ist, dass die Reihe konvergiert. Angewandt habe ich das Quotientenkriterium.

Wie sähe die korrekte Lösung aus?

Danke und VG

Edit:

Sehe gerade, dass es im Zähler oben doch eigentlich 1 + 1 * K! heißen muss oder? Wäre es dann am Ende 1 / (K+1) ?

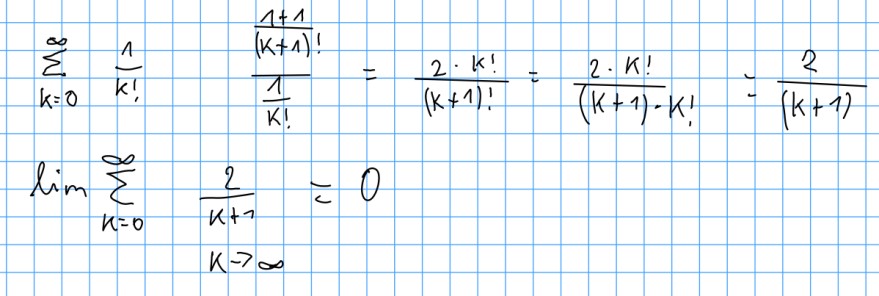
Text erkannt:

\( \begin{array}{l}\sum \limits_{k=0}^{\infty} \frac{1}{k !} \quad \frac{\frac{1+1}{(k+1) !}}{\frac{1}{k !}}=\frac{2 \cdot k !}{(k+1) !}=\frac{2 \cdot k !}{(k+1) \cdot k !}=\frac{2}{(k+1)} \\ \lim \limits_{k=0}^{\infty} \frac{2}{k+1}=0\end{array} \)

Answer 1

Wo kommt denn die 2 im Zähler her? Die ist falsch. Aber sonst passt es.

Kennst du auch den Grenzwert, der Reihe? Tipp: Im Zähler steht \( 1^k=1 \).

Comments

Danke für die Antwort.

1 hoch unendlich ist 1. Also 1 / unendlich. Läuft gegen 0. Den Grenzwert bei geometrischen Reihen kann ich ja berechnen. Hier aber kA.

VG

---

Wenn du den Grenzwert in der Aufgabe nicht berechnen musst, ist das auch egal. Falls du die Reihendarstellung der e-Funktion schon kennst, solltest du den Grenzwert aber angeben können.

---

Steht etwas im Skript dazu. Aber das muss ich mir noch anschauen.