Wie berechne ich diese aufgabe zu den ableitungen

Question

AufgabeErmitteln Sie, in welchen Punkten die Tangente an den Graphen von f parallel zur Geraden g mit
g (x) = x - 2 ist.
a) f(x) = 0,5 x²+ 1

b)f(x) = (x - 2) (x - 3) + 4
c) f(x) = 3x³ - 1/2x² + 1/3x

ich weiß nicht wie ich da angehen soll

Answer 1

Aloha :)

Die Gerade $\,g(x)=\pink1\cdot x-2\,$ hat die Steigung $m=\pink1$. Wir suchen also von den angegebenen Funktionen alle Punkte, an denen ihre erste Ableitung gleich $\pink1$ ist.

$$\text{zu a)}\quad f(x)=\frac12x^2+1\implies f'(x)=x$$$$1\stackrel!=f'(x)=x\implies x=1$$Der gesuche Punkt ist daher $A(1\big|\frac32)$.

$$\text{zu b)}\quad f(x)=(x-2)(x-3)+4=x^2-5x+10\implies f'(x)=2x-5$$$$1\stackrel!=f'(x)=2x-5\implies 2x=6\implies x=3$$Der gesuchte Punkt ist also $B(3|4)$.

$$\text{zu c)}\quad f(x)=3x^3-2x^2+3x\implies f'(x)=9x^2-4x+3$$$$1\stackrel!=f'(x)=9x^2-4x+3\implies9x^2-4x+2=0\implies9\left(x^2-\frac49x+\frac29\right)=0$$$$\qquad\qquad\implies x^2-\frac49x+\frac{18}{81}=0\implies\left(x^2-\frac49x+\frac{4}{81}\right)+\frac{14}{81}=0$$$$\qquad\qquad\implies\underbrace{\left(x-\frac29\right)^2}_{\ge0}+\frac{14}{81}=0\implies\text{keine Lösung}$$Es gibt keinen Punkt mit der Tangentensteigung $1$.

Answer 2

Die Gerade g hat die Steigung 1.

Gesucht werden die x bei denen die erste Ableitung der Funktionen ebenfalls gleich 1 ist.

D.h.m.a.W.:

Leite die Funktion f nach x ab, setze die Ableitung gleich 1 und löse die Gleichung nach x auf. Und da nach Punkten und nicht nicht nach Stellen gefragt wird, wird auch noch die y-Koordinate gesucht. Setze dazu die gefundenen x in f(x) ein.

Answer 3

Es muss gelten:

f '(x) = g '(x) , g'(x) = 1

a) x= 1

f(1) = 1,5

P(1/1,5)

Comments

könnten sie sich die c)einmal anschauen da komme ich wirklich garnicht weiter

Answer 4

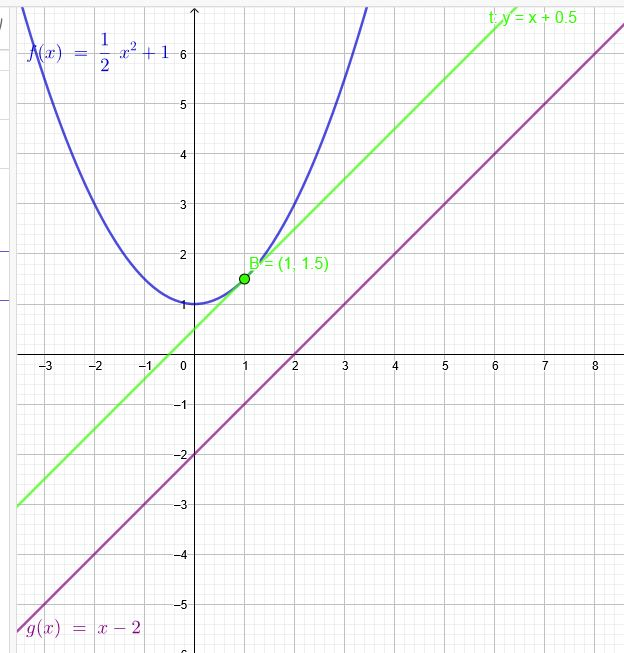
Ermitteln Sie, in welchen Punkten die Tangente an den Graphen von f parallel zur Geraden g mit
$g (x) = x - 2$ ist.
a) $f(x) = 0,5 x^2+ 1$

$0,5x^2+1= x - 2$  → $0,5x^2-x= - 3$ → $x^2-2x=- 6$

$x^2-2x+1=- 6+1=-5$

$(x-\red{1})^2=-5$

An der Stelle $x=\red{1}$  ist das der Fall.

$f(1) =1,5$  

$B(1|1,5)$

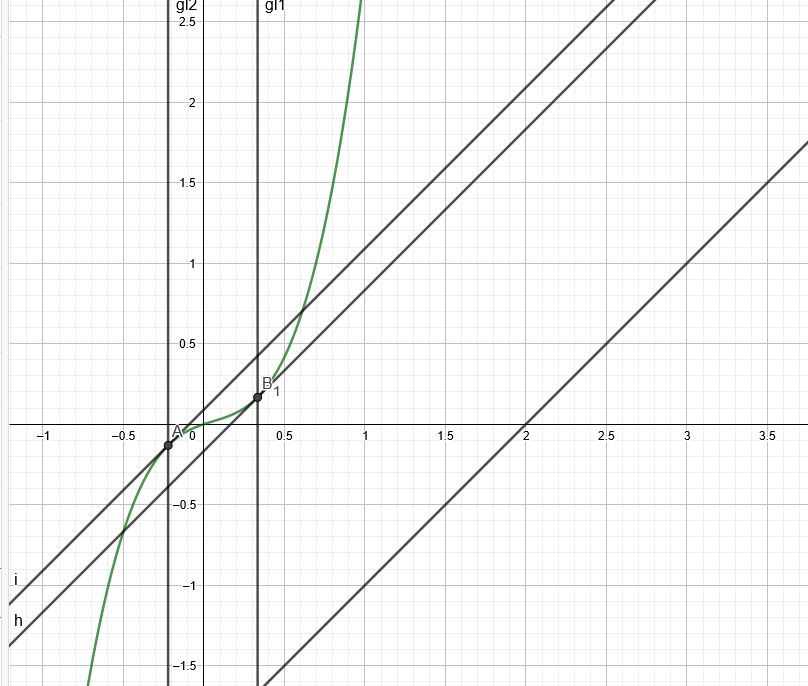
c) $f(x) = 3x^3 - \frac{1}{2}x^2 + \frac{1}{3}x$

$f'(x) = 9x^2 - x + \frac{1}{3}$   mit Steigung der Geraden $m=1$

$1 = 9x^2 - x + \frac{1}{3}$

$9x^2 - x - \frac{2}{3}=0|:9$

$x^2 - \frac{1}{9}x = \frac{2}{27}$

$x^2 - \frac{1}{9}x +(\frac{1}{18})^2= \frac{2}{27}+(\frac{1}{18})^2$

$(x - \frac{1}{18})^2= \frac{2}{27}+(\frac{1}{18})^2=\frac{25}{324}|±\sqrt{~~}$

1.)

$x - \frac{1}{18}=\frac{5}{18}$

$x_1=\frac{1}{3}$         $f(x_1) = ...$

2.)

$x - \frac{1}{18}=-\frac{5}{18}$

$x_2=-\frac{2}{9}$        $f(x_2) = ...$