Kann sich das mal jemand anschauen und mir sagen, ob die Lösung so passt und wenn ja wie kommt ihr genau drauf?

Question

Aufgabe:

Hallo, ich hab grad alles herumversucht, um auf die in quadr. Funktion wie in der Lösung zu kommen, allerdings ist die bei mir nie gleich und ich hab keine Ahnung an was das noch liegen kann. Kann sich das mal jemand anschauen und mir sagen, ob die Lösung so passt und wenn ja wie kommt ihr genau drauf?

Sollten ja eigentlich relativ schnell bestimmt sein.

Umformen, einsetzten aber passt nicht...

Bitte um eure Hilfe danke!!

Problem/Ansatz:

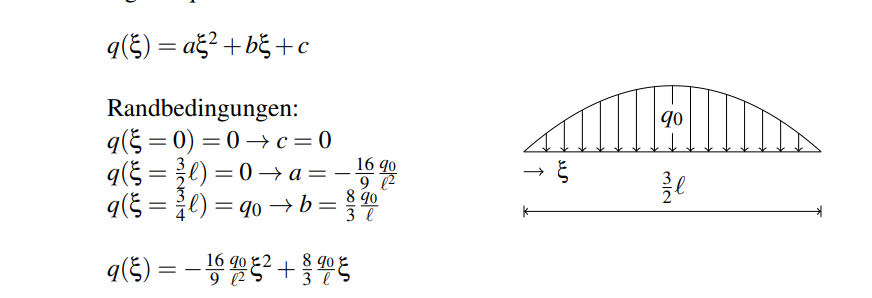
Text erkannt:

\( q(\xi)=a \xi^{2}+b \xi+c \)

Randbedingungen:
\( \begin{array}{l} q(\xi=0)=0 \rightarrow c=0 \\ q\left(\xi=\frac{3}{2} \ell\right)=0 \rightarrow a=-\frac{16}{9} \frac{q_{0}}{\ell^{2}} \\ q\left(\xi=\frac{3}{4} \ell\right)=q_{0} \rightarrow b=\frac{8}{3} \frac{q_{0}}{\ell} \\ q(\xi)=-\frac{16}{9} \frac{q_{0}}{\ell^{2}} \xi^{2}+\frac{8}{3} \frac{q_{0}}{\ell} \xi \end{array} \)

Answer 1

Stelle die Scheitelpunktform auf. Ich nutze dazu die eher Schulübliche Form

f(x) = - q0/(3/4·l)^2·(x - 3/4·l)^2 + q0

Das kann man so schon stehenlassen oder bei Bedarf ausmultiplizieren in die allgemeine Form

f(x) = 8/3·q0/l·x - 16/9·q0/l^2·x^2

Deine Funktion sieht also prima aus.