Aufgabe: Im Rahmen meiner Studienarbeit beschäftige ich mich Neuronalen Netzen. Das Grundprinzip ist mir bereits klar. Probleme hab ich aber mit dem mathematischen Verständnis der entstehenden Entscheidungsgrenze.
Hierfür würde ich gerne ein Beispiel nennen:
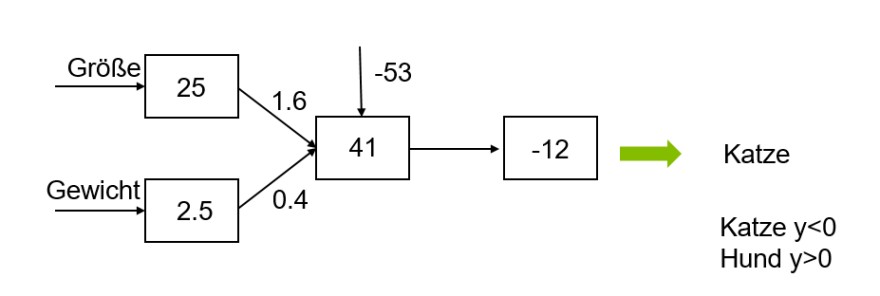
Mal angenommen ein sehr simples Neuronales Netz bestehend aus 2 Eingabe Neuronen, 1 Hidden Layer Neuron und 1 Ausgabe Neuron und soll anhand der Eingabe von Größe und Gewicht erkennen ob ein Tier ein Hund oder eine Katze ist.(Bild 1)
Durch die Eingabe entsteht ja eine Entscheidungsgrenze der Form y= ax+b, also eine lineare Entscheidungsgrenze. Für die Aufgabe umgewandelt ergibt sich: Tier = (a1 *Größe+ a2*Gewicht) + Bias.
Durch diese Entscheidungsgrenze werden aber auch kleine und leichte Hunde als Katzen erkannt. Man braucht also eine nicht-lineare Entscheidungsgrenzen.
Problem/Ansatz:
Und genau hier versteh ich es dann nicht mehr wirklich. Würde man jetzt immer mehr Hidden Layer Neuronen dran packen würde das doch nur die Zahlen a, x und b verändern, die Funktion bleibt doch weiterhin linear, oder?
Laut meiner Recherche ist die Aktivierungsfunktion also z.B. die ReLu oder Sigmoidfunktion dafür verantwortlich, dass die Entscheidungsgrenze nicht-linear wird. Ich versteh aber nicht wie das funktionieren soll.
Wie wird aus einer linearen Entscheidungsgrenze eine nicht-lineare durch die Aktivierungsfunktion? Wird die lineare Funktion verändert oder was passiert da genau?