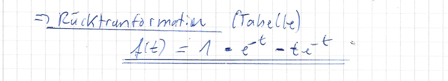Laplace Transformation mit Anfangswert lösen

Question

Aufgabe 1:

a) Gegeben sei die Anfangswertaufgabe
\( u^{\prime \prime}-2 u^{\prime}+u=\sin (4 t)+2 t e^{-t} \text {, für } t>0, \quad u(0)=1, u^{\prime}(0)=0 . \)

In welche algebraische Gleichung lässt sich die Anfangswertaufgabe durch die Laplace-Transformation überführen?
Bitte belegen Sie Ihre Antwort durch Zwischenrechnungen.
Berechnen Sie die Lösung der algebraischen Gleichung.
b) Es sei \( F(s)=\frac{1}{s(s+1)^{2}} \) die Laplace-transformierte der Funktion
\( f: \mathbb{R}_{0}^{+} \rightarrow \mathbb{R}, \quad f: t \mapsto f(t) . \)

Bestimmen Sie \( f(t) \).

Problem:

Leider weiß ich hier nicht weiter

Comments

Wo weißt Du nicht weiter? Direkt nach Lesen der Aufgabe kapituliert? Wende die LT auf die Dgl an. Beispiel war sicher in der Vorlesung dran.

Answer 1

Hallo,

a)

Ansatz folgt aus dem Differentationssatz:

u=F(s)

u'= -u(0) +s F(s)

u''= -s u(0) -u'(0) +s^2 F(s)

Setzte das in die DGL ein .Von der rechten Seite der DGL mußt Du eine LP-transformation via Tabelle machen.

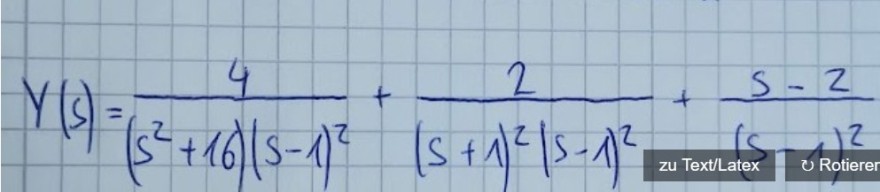
das stimmt bisher, das kannst Du weiterbearbeiten mit der Einsetzmethode wie unter b

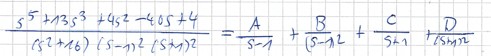
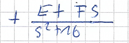
Du kommst dann auf:

Y(s)= \( -\frac{9}{34(s-1)^{2}}+\frac{273}{578(s-1)}+\frac{1}{2(s+1)^{2}}+\frac{1}{2(s+1)}-\frac{60}{289\left(s^{2}+16\right)}+\frac{8 s}{289\left(s^{2}+16\right)} \)

dann kannst Du via Tabelle zurücktransformieren

\( u(t)=\frac{273 e^{t}}{578}+\frac{e^{-t}}{2}-\frac{9 e^{t} t}{34}+\frac{e^{-t} t}{2}+\frac{8}{289} \cos (4 t)-\frac{15}{289} \sin (4 t) \)

b)

Führe eine Partialbruchzerlegung aus:

Ansatz

\( \frac{1}{s (s+1)^2} \) =\( \frac{A}{s} \) +\( \frac{B}{s+1} \) +\( \frac{C}{(s+1)^2} \)

danach Rücktransformation via Tabelle

Comments

Text erkannt:

\( Y(s)=\frac{4}{\left(s^{2}+16\right)(s-1)^{2}}+\frac{2}{(s+1)^{2}(s-1)^{2}}+\frac{s-2}{(s-1)^{2}} \)

Leider weiß ich nicht, wie man in b) die Partialbruchzerlegung angeht.