Aufgabe:

Text erkannt:
Gegeben ist die in \( I R \backslash\{0\} \) definierte Funktion \( f: x \mapsto 1-\frac{1}{x^{2}} \), die die Nullstellen \( x_{1}=-1 \) und \( x_{2}=1 \) hat. Die Abbildung zeigt den Graphen von \( \mathrm{f} \), der symmetrisch bezüglich der \( y \)-Achse ist. Weiterhin ist die Gerade g mit der Gleichung \( y=-3 \) gegeben.
a Zeigen Sie, dass einer der Punkte, in denen g den Graphen von \( f \) schneidet, die \( x \)-Koordinate \( \frac{1}{2} \) hat.
b Bestimmen Sie rechnerisch den Inhalt der Fläche, die der Graph von f, die x-Achse und die Gerade g einschließen.
Ich habe bei der b) Probleme.
Ich habe zunächst einmal folgendes berechnet:
A= 2*integral(von f(x) - g(x); untere Grenze = -1.5 ; obere Grenze = 0)
Habe dann aber erkannt, dass es nicht so geht da bei Einsetzen der Grenzen,
A= 2*Integral(4x+x^-1) ... stehen würde. Also die obere Grenze 0 kann natürlich nicht eingesetzt werden, da nicht durch
Null geteilt werden kann.
Warum ist das so?
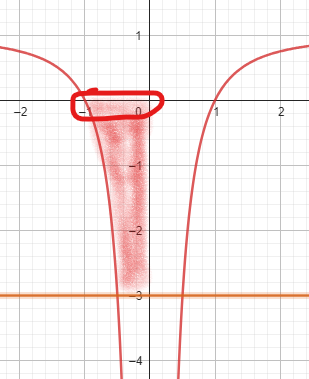
Ist meine Begründung richtig, dass es so ist, weil die Fläche nicht ganz eingeschlossen ist?
Die Fläche würde ja sonst über die x-Achse gehen und nie aufhören quasi bis y= unendlich
Und meine zweite Frage ist, welche Möglichkeit gibt es, die Fläche zu berechnen?