Aufgabe:
3.5 Sei \( \mathcal{A} \) eine Familie \( k \)-elementiger Teilmengen von \( N=\{1,2, \ldots, n\} \). Der Schatten \( \Delta \mathcal{A} \) ist die Familie aller \( (k-1) \)-elementigen Teilmengen von allen Mengen aus \( \mathcal{A} \), d.h.
\( \Delta \mathcal{A}:=\left\{Y \in\binom{N}{k-1}: \exists X \in \mathcal{A} \text { mit } Y \subset X\right\} . \)
Man beweise:
\( \frac{|\mathcal{A}|}{\binom{n}{k}} \leq \frac{|\Delta \mathcal{A}|}{\binom{n}{k-1}} \)
Ansatz: 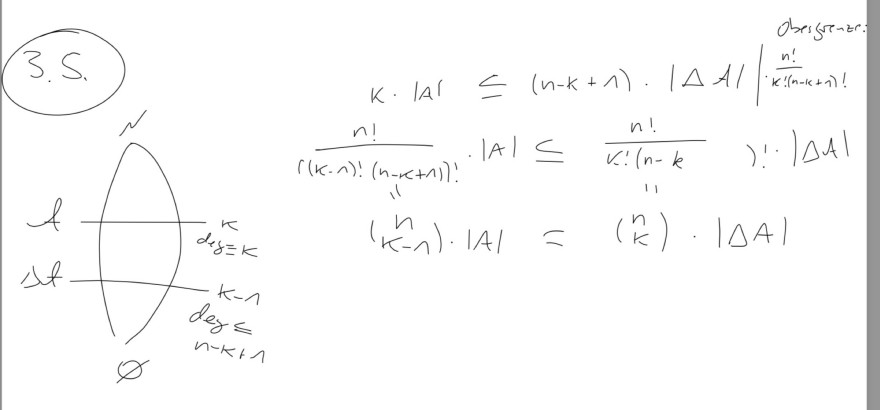
Text erkannt:
\( \begin{aligned} k \cdot|A| & \leq\left.(n-k+1) \cdot|\Delta A|\right|^{\frac{\text { obeastrente! }}{n!} \cdot \frac{n!(n-k+1)!}{}} \\ \frac{n!}{(k-1)!(n-k+1)!} \cdot|A| & \left.\leq \frac{n!}{k!(n-k}\right)!\cdot|\Delta A| \\ \binom{n}{k-1} \cdot|A| & =\binom{n}{k} \cdot|\Delta A|\end{aligned} \)
Kann mir jemand die Lösung erklären?