Wie zeichnet man den Graphen der Ableitungsfunktion bei der zweiten Funktion?

Question

Aufgabe:

Graphen skizzieren (Ableitungsfunktion)

Problem/Ansatz:

Moin,
ich habe bei der dritten Aufgabe ein kleines Problem
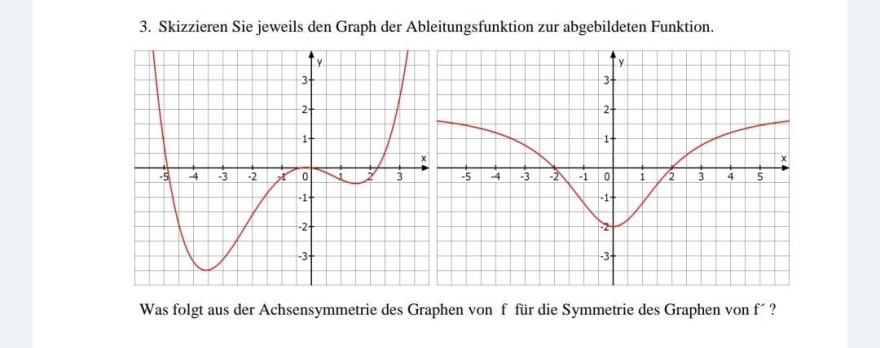
Wie zeichnet man den Graphen der Ableitungsfunktion bei der zweiten Funktion? Ich sehe dort nur einen Tiefpunkt an der Stelle 0 und bin unsicher, wie ich den Graphen entsprechend zeichnen soll.
Bild zum Beitrag
Vielleicht ergibt sich daraus ja auch gleich die Antwort auf die Frage weiter unten: „Was folgt aus der Achsensymmetrie des Graphen?“

Text erkannt:

3. Skizzieren Sie jeweils den Graph der Ableitungsfunktion zur abgebildeten Funktion.

Was folgt aus der Achsensymmetrie des Graphen von f für die Symmetrie des Graphen von \( \mathrm{f}^{\prime} \) ?

Comments

Orientiere Dich an der Steigung. f fällt von -∞ bis Null, also ist die Steigung und somit die Ableitung …

Analog auf der rechten Seite; dann wo ist die Steigung Null und wo hat f wendepunkte und was bedeutet das für die Ableitung? Dann solltest du da sein….Die Symmetrie siehst Du dann auch oder Du überlegst sie dir vorher…

Answer 1

Der Graph der Funktion zeigt einen Tiefpunkt an der Stelle x=0. Der Graph der Ableitungsfunktion muss an dieser Stelle eine Nullstelle mit einem Vorzeichenwechsel von Minus nach Plus besitzen. Im einfachsten Fall sieht der Graph der Ableitung dort also so aus: "\".

Vielleicht ergibt sich daraus ja auch gleich die Antwort auf die Frage weiter unten: „Was folgt aus der Achsensymmetrie des Graphen?“

Ja.

Comments

Nicht eher / ?

---

Das wollte ich nicht ausschließen!

Answer 2

Mache dir einmal folgenden Zusammenhang deutlich: Die Ableitungsfunktion \(f'\) gibt die Steigung des Graphen von \(f\) an. Wenn der Graph von \(f\) also fällt, ist die Ableitung negativ. Steigt der Graph, ist die Ableitung positiv.

Du kannst ja auch mal mit deinem Geodreieck Tangenten an den Graphen legen und ungefähr die Steigung ablesen (Steigungsdreieck). Das machst du für mehrere Punkte und dann solltest du erkennen können, wie die Ableitung in etwa aussieht.