Wie funktioniert Polynomdivision (CRC)?

Question

Folgende Aufgabenstellung:

Es handelt sich um das Thema zyklische Redundanzprüfung. Gegeben sind ein übertragener Frame inklusive redundanten Bits sowie das dazu gehörige Generatorpolynom.Der Frame wurde über ein Netzwerk übertragen und von einem Empfänger erhalten. Die Aufgabenstellung besteht aus zwei Teilen:
1. Berechnung, ob der Frame fehlerfrei übertragen wurde.
2. Angabe der Eigenschaften des gegebenen Generatorpolynoms.

 

Wie die Polynomdivision (CRC) funktioniert habe ich soweit verstanden. 
Allerdings verstehe ich folgendes nicht ganz:
Ich habe 10101000000 als Frame und 1000 als Generatorpolynom.
Die eigentliche Rechnung ist ja nicht weiter schwer, allerdings verstehe ich nicht, warum und wie oft man Nullen anhängen muss.

 

Warum müssen da 3 Nullen angehangen werden? Warum nicht mehr bzw. warum überhaupt eine?

Answer 1

Betrachte erst

x⁷ : x = x⁶ + 0x⁵ + 0x⁴ + 0x³ + 0x² + 0x + 0 = x⁶

Analog

6'000'000 : 2 = 3 warum braucht es hier noch 6 Nullen?

6'000'000 : 2 = 3*1'000'000 + 0*100'000 + 0*10'000 + 0*1000 + 0*100 + 0*10 + 0*0 = 3'000'000
6
00
  00
    00
 .......
 

Beispiel:

10000 (2er-System) =1* 2^5-1 = 2⁴ = 16 (10erSystem).

Ich hoffe das klärt dein Verfahren etwas.

 

Dasselbe gilt im 2er-System, das ebenfalls ein Positionssystem ist. Statt x^n-1 oder 10^n-1 hast du im Dualsystem 2^n-1 als Faktor dazuzudenken, wenn du die Werte einer Zahl mit mehreren Stellen ansiehst.

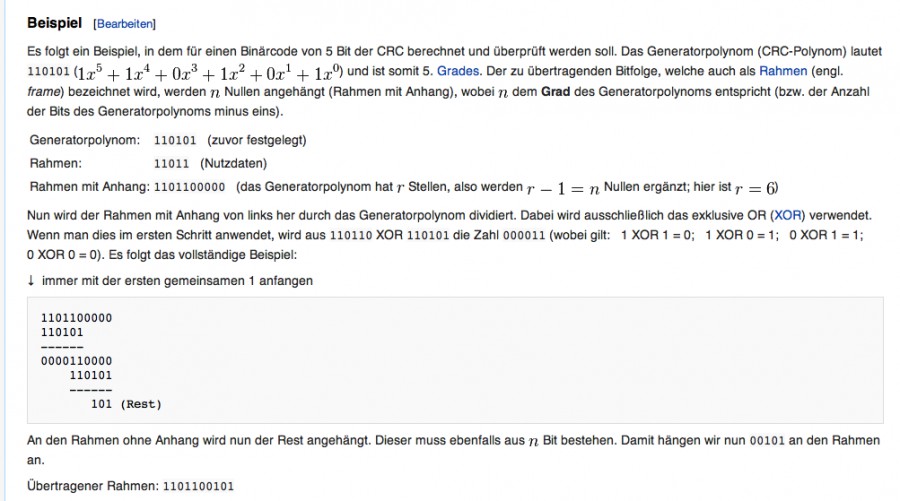
Vgl. auch hier: https://de.wikipedia.org/wiki/Zyklische_Redundanzprüfung

Du hast ja den Generator und den Frame: Die zu übertragende Kette wird als Generator * Frame berechnet. Ihre Längen müssen sich praktisch addieren. Genauer: Die Länge ist deren Summe minus 1. Beispiel im 10erSystem richtige verschlüsselte Mitteilung: 100 * 34 = 3400 hat die Länge 3+2-1=4.

Beispiel im angegebenen Wikipedialink: