Aufgabe 2: Kostenfunktion
Ein Hersteller von Designerleuchten möchte ein neues Lampenmodell produzieren. Um damit einen Gewinn zu erzielen, stellt er zunächst Überlegungen zu den Gesamtkosten der Produktion und dem Verkaufspreis der Lampen an. Die Gesamtkosten der Produktion in Abhängigkeit von der Stückzahl schätzt der Hersteller aufgrund seiner bisherigen Erfahrungen mit der Kostenfunktion \( K \) ab. Der Graph von \( K \) ist in der Abbildung 1 dargestellt.
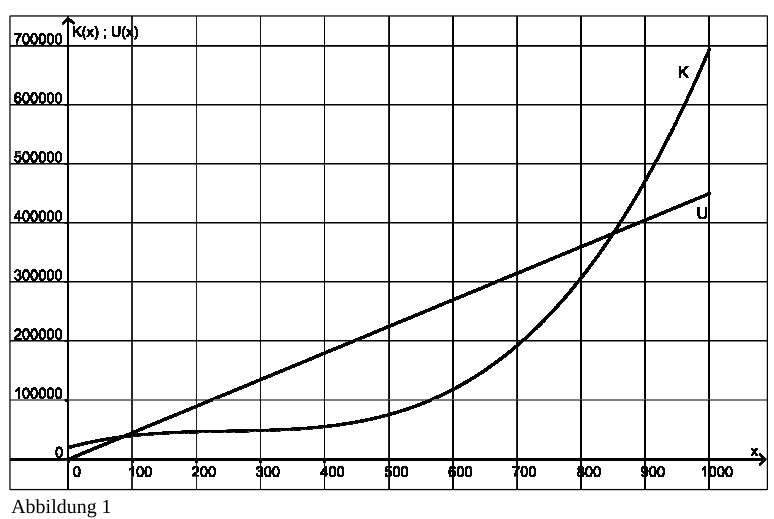
Die Funktionsgleichung von \( K \) ist
$$ K(x)=0,0015 \cdot x^{3}-1,125 \cdot x^{2}+298,8 \cdot x+20000 \text {. } $$
Dabei bezeichnet
\( x \) : die Anzahl der produzierten Lampen
\( K(x): \) die Gesamtkosten für die Produktion von \( x \) Lampen in Euro.
Mit der Funktion \( K \) ist es möglich, die Aufgabenteile a) bis e) zu beantworten. Die Untersuchungen werden im Folgenden auf den Bereich \( 0 \leq x \leq 1000 \) beschränkt, d. h. es sollen nicht mehr als 1000 Lampen produziert werden.
a) Berechnen Sie die Gesamtkosten, die für 560 produzierte Lampen anfallen.
b) Die Kostenfunktion \( K \) besitzt keine lokalen Extremstellen.
[Hinweis: Diese Tatsache sollen Sie nicht nachweisen.]
Begründen Sie, dass diese Tatsache im Sachzusammenhang sinnvoll ist.
c) (1) Bestimmen Sie rechnerisch die Wendestelle \( x_{W} \) der Kostenfunktion K.
[Zur Kontrolle: \( x_{W}=250 \) ]
(2) Für \( x>250 \) ist der Graph der Kostenfunktion \( K \) linksgekrümmt.
Erklären Sie die Bedeutung dieser Tatsache im Sachzusammenhang.
Aufgrund einer Marktanalyse geht der Hersteller davon aus, dass er jede produzierte Lampe zu einem Stückpreis von \( 450 \in \) verkaufen kann. Wenn er \( x \) Lampen produziert, kann der Hersteller also durch die Funktion \( U \) mit \( U(x)=450 \cdot x \) berechnen, wie viel Geld er von seinen Kunden insgesamt erhält. Dieser Geldbetrag wird als Umsatz des Herstellers bezeichnet.
d) Der Graph der Umsatzfunktion \( U \) ist in Abbildung 1 dargestellt.
Bestimmen Sie aus der Abbildung 1 näherungsweise, bei welchen Produktionsmengen der Hersteller einen Gewinn macht, und begründen Sie Ihr Ergebnis.
e) Aus der Umsatzfunktion \( U \) und der Kostenfunktion \( K \) ergibt sich die Gewinnfunktion \( G \), mit der sich der Gewinn \( G(x) \) berechnen lässt.
(1) Weisen Sie durch eine geeignete Berechnung nach, dass für die Funktionsgleichung von G gilt:
$$ \begin{array}{l} G(x)=-0,0015 \cdot x^{3}+1,125 \cdot x^{2}+151,2 \cdot x-20000 \\ (0 \leq x \leq 1000, G(x) \text { in Euro) } \end{array} $$
(2) Ermitteln Sie rechnerisch, bei welcher Anzahl an produzierten Lampen der Gewinn maximal ist.
Ansatz/Problem:
Die letzten 2 Aufgaben leuchten mir nicht ganz ein. ich vermute das man bei der letzten Aufgabe das Gleichsetzungsverfahren anwenden muss.