Hallo :)
Ich habe zuvor eine sehr ähnliche Aufgabe gestellt. Ich wäre euch sehr dankbar, wenn ihr mir auch bei dieser Aufgabe helfen könntet. Könnte ihr mir sagen, welche die Funktionen die richtigen sind und vorallen WISO =)
Ich weiss die Aufgabe ist sehr ähnlich aber meine Klassen Kamaraden haben es mir auch schon probiert zu erklären. Mit diesen ähnlichen Aufgaben kann ich es vielleicht durch vergleiche entlich verstehen ^^
Vielen lieben Dank :))
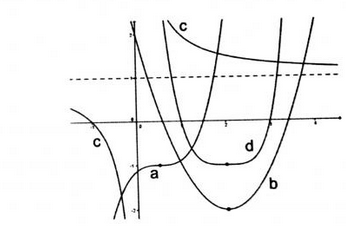
Finden Sie für die vier gezeichneten Graphen die richtige Funktionsgleichung.
\( y_{1}=-(x+2)^{2}+2 \quad y_{2}=-(x-2)^{2}-2 \)
\( y_{3}=(x+2)^{2}+2 \quad y_{4}=(x-2)^{2}-2 \)
\( y_{5}=(x-0.5)^{3}-1 \quad y_{6}=-(x+0.5)^{3}+1 \)
\( y_{7}=(x+0.5)^{3}-1 \quad y_{8}=(x-0.5)^{3}+1 \)
\( y_{9}=(x-2)^{4}-1 \quad y_{10}=(x+2)^{4}-1 \)
\( y_{11}=(x-2)^{4}+1 \quad y_{12}=(x+2)^{4}+1 \)
\( y_{13}=x^{-1}+2 \quad y_{14}=x^{-2}+1 \)
\( \mathrm{y}_{15}=\mathrm{x}^{-2}-1 \quad \mathrm{y}_{16}=\mathrm{x}^{-1}+1 \)