Hier mal die Antwort zur Gleichung:
Löse die Gleichung graphisch: 4 - (x + 2)2 = 0
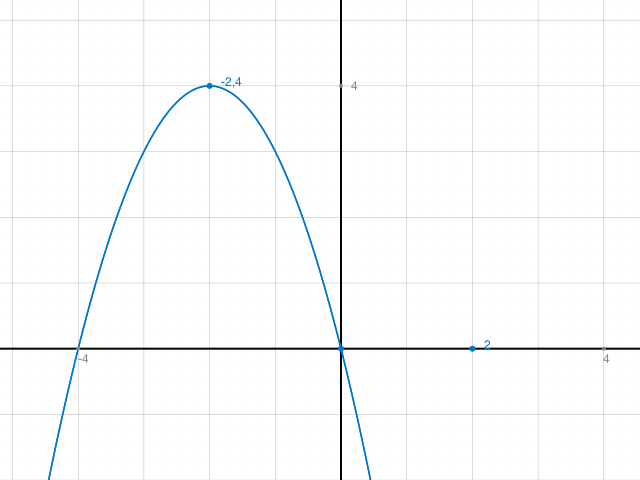
y= - (x + 2)2 + 4 |Graph: nach unten geöffnete Normalparabel mit Scheitelpunkt in S(-2|4)
y = 0 |Graph: x-Achse
Beim Zeichnen der Parabel darauf achten, dass 1 → 1 , 2--> 4, 3--->9 gilt.
Also von (-2,4) aus 1 nach rechts und links und 1 runter: 2 Punkte
2 nach rechts und links und 4 runter: 2 Punkte
Diese beiden liegen auf der x-Achse. Dort die Lösungen ablesen
x1 = -4, x2 = 0.
Probe (Rechnung) 0 = - (-2)^2 + 4 und 0 = -(2)^2 + 4 ? ok.
1) Alkohol wird annähernd linear abgebaut. Bei Verkehrsdelikten rechnen Rechtsmediziner im Normalfall damit, dass der im Blut vorhandene Alkohol um 0,1 Promille pro Stunde abnimmt.
a) Ein 70 kg schwerer Mann trinkt 1 Liter Bier, was bei ihm zu einem Blutalkoholgehalt von ca. 0,8 Promille führt. Der Alkoholabbau beginnt erst 2 Stunden später.
Gib eine Termdarstellung der Funktion A an, die jedem Zeitpunkt t den Blutalkoholgehalt A(t) in Promille zuordnet! Skizziere den Graphen der Funktion!
0.1 Promille Abnahme pro Stunde bedeutet: Steigung m ist -0.1
A(t) = - 0.1 t + q
Anfangswert zu Beginn des Abbauprozesses
A(2) = - 0.1 * 2 + q = 0.8 |+ 0.2
q = 1
Also A(t) = -0.1 t + 1
b) Nach welcher Zeit ist der gesetzlich erlaubte Höchstwert von 0,5 Promille erreicht?
Nach 5 Stunden (Stimmt oder?)
Gleichung mit A(t)
-0.1 * t + 1 = 0.5 |-1
-0.1 * t = - 0.5 |:(-0.1)
t = 0.5/0.1 = 5. Deine Antwort stimmt.