Kostenumschlüsselung: 1.000 Flyer kosten 1082 €.

Question

kann mir jemand bitte den Lösungsweg zu folgender Aufgabe aufzeigen?

Aufgabe:

1.000 Flyer kosten 1082 €

5.000 Flyer kosten 3075 €

Wieviel kosten 3.000 Flyer?

 :-)!

Comments

Offenbar besteht kein proportionaler Zusammenhang zwischen Stückzahl und Kosten. Eine Lösung über einen Dreisatz kommt also nicht in Frage. Gehen wir davon aus, dass sich die Flyer-Kosten aus stückzahlunabhängigen Fixkosten und stückzahlabhängigen variablen Kosten zusammensetzen, hätten wir eine lineare Kostenfunktion, von der wir zwei Wertepaare kennen. Damit ist die Kostenfunktion eindeutig bestimmbar und wir könnten mit ihr die Flyer-Kosten für beliebige Stückzahlen berechnen.

Das wollen wir aber nicht, sondern wir wollen nur die Kosten für genau 3000 Flyer (das liegt in der Mitte zwischen 1000 Flyern und 5000 Flyern) berechnen...

Answer 1

1,082 * 3000 = 3246 €

Comments

Legendär !!

hier hat es mal wieder jemand mit einer doppelt falschen Antwort auf deine Punkte abgesehen

---

Bei dir möchte ich kein Kunde sein.

5000 Flyer kosten 3075 € laut Aufgabe.

Bei dir kosten 3000 Flyer 3246 €.

Es gibt zwar für Mindermengen eine Aufschlag, deiner ist aber gesalzen.

---

und wie ist jetzt der richtige Lösungsweg :)?

---

Hast du noch zusätzliche Angaben zur Aufgabe. Handelt es sich um ein Angebot mit Fixkosten und Produktionskosten je Stück ( Flyer)

Lautet die Frage:

Wieviel (Flyer) kosten 3.000 €?

---

richtig, hierbei handelt es sich um ein Angebot mit fixen und variablen kosten. Leider habe ich die genauen Angaben nicht... Mir geht es nur grundsätzlich um den lösungsweg mittels Dreisatz. Hier geht es nicht um eine exakte Kostenermittlung, sondern nur um einen "ungefähren" Wert. Die Frage lautet: "Was kosten 3000 Flyer"

Danke für deine Mühe

---

K(x)=ax+b

hier wäre es mir zu aufwendig, in meiner Kalkulationsbasis die fixen und variablen Kosten aufzuschlüsseln.

Answer 2

Um eine Kostenfunktion auzustellen fehlt leider noch mindestens eine Angabe.

Hier eine Milchmädchenrechnung:

[ (1082 + 3075) : 6000 ]*3000  ≈ 2078,5

Comments

Bei der naheliegenden Unterstellung einer linearen Kostenfunktion werden keine weiteren Angaben benötigt. Die Kostenfunktion selbst muss zum Beantworten der Fragestellung nicht einmal ermittelt werden...

---

Von einer linearen Kostenfunktion  habe ich nichts geschrieben,  da der Durchschnittspreis des einzlenen Flyers sich ja senkt, kann man es noch mit antiproportionaler Zuordnung probieren.

---

Ich wollte damit ausdrücken, dass es naheliegend ist, eine lineare Kostenfunktion zu unterstellen. Siehe dazu meinen Kommentar, der als zweiter unter der Frage steht. Damit ist die Aufgabe auf jeden Fall eindeutig und allgemein lösbar. Soweit muss man aber gar nicht gehen, die gegebene Aufgabe lässt sich wesentlich einfacher lösen.

Eine Lösung über einen Dreisatz ist hier nicht möglich, ohne vorher die Fixkosten herauszurechnen.

Hier einen antiproportionalen Zusammenhang zu sehen, finde ich eher abenteuerlich.

Answer 3

Hm , dann antworte ich auch mal :D

1000 F= 1082€

5000 F.= 3075€

10 F = 10,82€9

70 F = 75,74€


Da 5000 F. genau 75€ zu viel kosten, ziehen wir 70 F ab und haben somit: 4930 F. (Das ungenau)

Allerding ist die AUfgabe auch etwas seltsam. 1000 F = 1082€ und 5000 F = 3075€. Mengenrabatt???

Answer 4

Hier mein Versuch einer Lösung:

Da in den Stichworten zur Frage "Dreisatz" als erstes vorkommt, könnte man davon ausgehen, dass hier der Dreisatz gemeint sei.

Bestimmen wir zuerst den Preis je Flyer:

1.000 Flyer kosten 1082 € → 1 Flyer = 1,082 €

5.000 Flyer kosten 3075 € → 1 Flyer = 0,615 €

Hier haben wir jedoch einen veränderten Flyerpreis. Damit kann es sich nicht um den Dreisatz und proportionale Zuordnung handeln.

Gehen wir stattdessen von einer linearen Funktion aus, die den Flyerpreis wiedergibt, erhalten wir folgende Funktionsgleichung:

f(x) = 0,49825*x+583,75

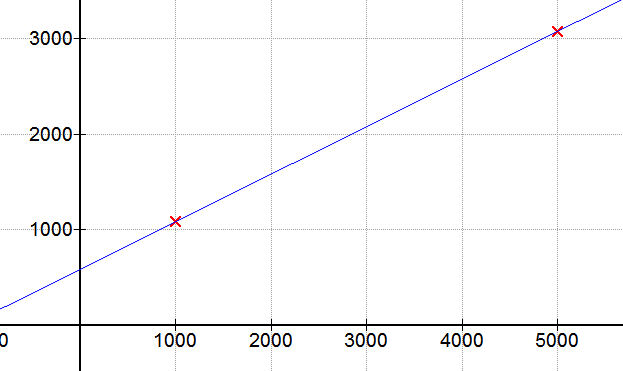
Damit erhalten wir bei 3000 Flyern:

f(3000) = 0,49825*x+583,75 = 2078,50 €

Diesen Wert hat bereits Mitglied Akelei bestimmt.

Comments

Na ja, die Beobachtung, dass 3000 Flyer gerade in der Mitte zwischen 1000 Flyern und 6000 Flyern liegen, erlaubt die Bestimmung der Kosten für 3000 Flyer über den Mittewert, hier also
(1082 € + 3075 €) : 2 = 2078,50 €

Es ist auchmöglich, unmttelbar mit den beiden Zeilen aus der Aufgabenstellung weiter zu rechnen:

1.000 Flyer kosten 1082 €

5.000 Flyer kosten 3075 €

6.000 Flyer kosten 4157 €

3.000 Flyer kosten 2078,50 €

---

Es soll aber nicht unerwähnt bleiben, dass die letzet Lösung nicht sehr schön ist:

1.000 Flyer kosten 1082 €

5.000 Flyer kosten 3075 €

6.000 Flyer kosten 4157 €   ←   Hier sind die Fixkosten zweifach enthalten

3.000 Flyer kosten 2078,50 €   ←   Hier stimmt es dann wieder.