Stellen Sie f graphisch dar f(x) = (x²+2x-3)/(x²+x-2)

Question

Gegeben sei die Funktion 

f: x-> (x²+2x-3)/(x²+x-2); x E D f

a) Bestimmen sie Definitionsbereich, Nullstellen, Polstellen, Asymptoten, Grenzwerte und Näherungsverhalten der Funktion f 

b) Stellen sie f graphisch dar

Answer 1

untersuche den Nenner auf Nullstellen:

x^2+x-2 = 0   |pq-Formel

x₁ = -2 und x₂ = 1

--> D = ℝ\{-2;1}

Nullstellen des Zählers:

Wieder pq-Formel

x^2+2x-3 = 0 

x₁ = 1 und x₂ = -3

Polstellen:

Da sich die beiden Nullstellen mit x = 1 weg heben, haben wir nur eine Polstelle bei x = -2.

Nullstellen:

Da sich x = 1 weghebt ist x = -3 keine Nullstelle (sondern eine hebbare Definitionslücke.

Asymptote:

Waagerecht: y = 1

Senkrecht: x = -2

Grenzwerte/Verhalten:

Für x->±∞ haben wir 1

Bei der Polstelle sind wir links davon negativ, rechts davon positiv gegen ∞.

Das kann man auch in ein Schaubild übertragen:

 

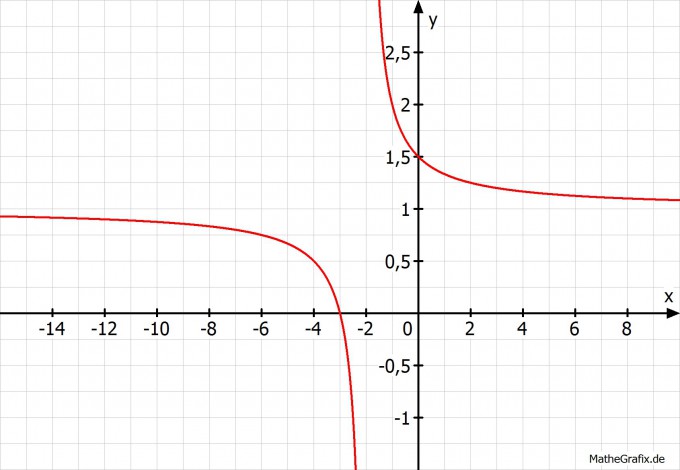
Grüße