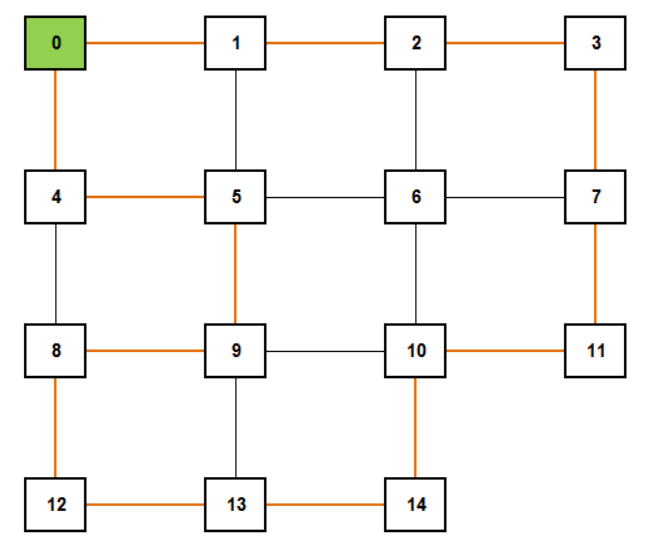
Graph mit den Knoten 0 bis 14
Der Knoten 0 ist der einzige Ein- und Ausgang des Labyrinths (Graph).
Bedingungen:
1. Nur der Knoten 0 muss genau zweimal besucht werden, einmal beim Betreten des Labyrinths und einmal beim Verlassen des Labyrinths.
2. Jeder andere Knoten muss genau einmal besucht werden.
Frage: Gibt es eine solche Route? Beweisen Sie Ihre Aussage.
Meine Antwort:
Nein es gibt keine Route, wenn alle Knoten genau einmal besucht werden bis auf die Ausnahmen mit dem Knoten 0.
Beweis:
Aus den beiden Bedingungen:
1. Nur der Knoten 0 muss genau zweimal besucht werden, einmal beim Betreten des
2. Jeder andere Knoten muss genau einmal besucht werden.
folgt: Es muss genau ein einfacher Kreis existieren und zwar mit dem Star- und End-Knoten 0.
Beim Traversieren aller Knoten entsteht jedoch mindestens ein weiterer Kreis, nämlich der mit dem Pfad (2, 3, 7, 11, 10, 6, 2). Da der Knoten 2 mehrfach besucht wird, erfüllt die Route die zweite Bedingung nicht.
Deshalb gibt es keine Route mit den Bedingungen 1 und 2.
Ist der Beweis richtig?
Eine Route ohne den Knoten 6 ist auf dem Labyrinth in Orange eingezeichnet.