Tipp: Lineare Gleichungssysteme ab sofort schneller lösen / Neues Tool schlägt Wolframalpha

Question

Update März 2018: Neuer Rechner LGS-Pro verfügbar!

Ihr kennt das sicher: Schon wieder eine Frage zu einem linearen Gleichungssystem, schon wieder sind nur die Lösungen gefragt.

Zur Lösung oder zur Kontrolle der eigenen Berechnungen könnt ihr jetzt das neue Matheprogramm: Lineare Gleichungssysteme online lösen verwenden.

Es ist hilfreich und scheint sogar mächtiger als Wolframalpha, wenn es sich um 5 Unbekannte handelt: Wolframalpha vs. LGS-Löser.

Screenshot:

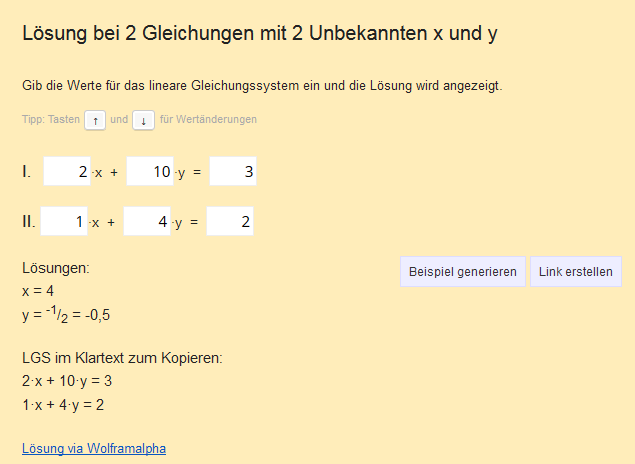
Lösbar sind LGS mit 2, 3, 4 und 5 Unbekannten. 

Zusätzlich lässt sich das LGS mit Lösungen bequem herauskopieren.

Hier eine Beispiel-Berechnung eines LGS mit 4 Unbekannten: 

-2·w – 8·x + 6·y + 8·z = 2
5·w + 1·x + 2·y – 1·z = 8
-3·w – 4·x + 1·y – 4·z = -7
9·w + 4·x – 3·y + 0·z = 9

Lösungen:
w = ³³/₃₂ = 1,03125
x = ²⁷/₃₂ = 0,84375
y = ³⁹/₃₂ = 1,21875
z = ⁷/₁₆ = 0,4375

Weitere Features:

- Lösungen werden ggf. als Brüche und als Kommazahlen dargestellt (ggf. gerundet).

- LGS lassen sich mit zufälligen Werten erstellen, Button "Beispiel generieren" klicken.

- Jedes LGS lässt sich speichern, einfach auf den Button "Link erstellen" klicken. 

- Jeder Wert kann mit Cursortasten verändert werden.

- Zur Kontrolle kann ein Link zu Wolframalpha herangezogen werden.

Ich denke, damit solltet ihr ab sofort noch schneller arbeiten können und wertvolle Zeit sparen.

Für Rückfragen oder Hinweise bitte kommentieren.

Vielen Dank,
Kai

Comments

Es gibt leider im Fall der nicht eindeutigen Lösung keine Auskunft darüber, ob es keine Lösung oder unendlich viele Lösungen gibt. In diesem Fall hilft Wolframalpha weiter.

Wird es diesbezüglich eine Erweiterung geben?

---

Das ließe sich bestimmt einbauen, ich müsste nur noch einen passenden Algorithmus finden. Der LGS-Löser arbeitet mit der Cramerschen Regel, d. h. wenn die Determinante Null ist, dann ist das LGS nicht definiert. Leider kann man jedoch daran nicht erkennen, ob A unendliche viele Lösungen oder B keine Lösung existiert.

Gerade gefunden: Es soll möglich sein, vgl. Bestimmung über die erweiterte Koeffizientenmatrix, das scheint jedoch komplex, da man hierzu das gesamte LGS umformen muss.

Vielleicht geht es noch einfacher, vgl. Frage hier.

---

Für das LGS mit 2 Unbekannten habe ich es eingebaut (hier muss man nur auf Vielfache prüfen), Beispiel für unendlich viele Lösungen hier.

---

@Gast: Die Anzahl der Lösungen wird nun auch angezeigt. Dazu wird im Hintergrund der Anwendung das Gaußverfahren verwendet.

Answer 1

Hallo Kai, hast du das programmiert ?

Comments

Ja, mit Hilfe der Cramerschen Regel ging es besser als erwartet.

Bisher stammen alle Programme der Assistenzrechners von mir (Stand Dez. 2017).