Ich habe mal dein Bild bearbeitet: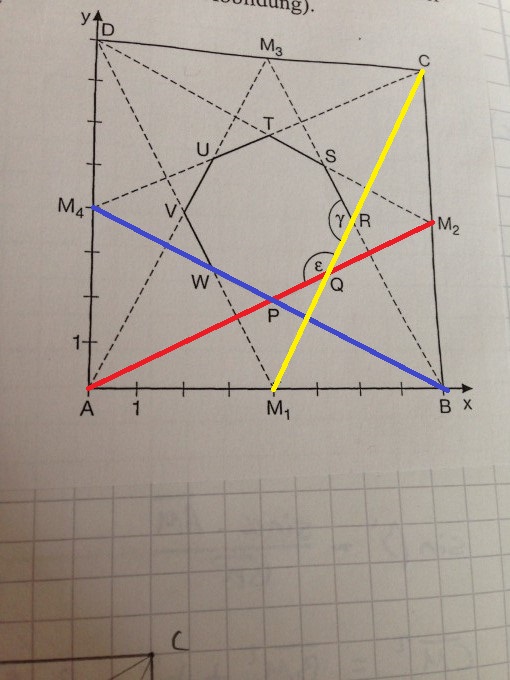
Die Graden waren vorher ja auch schon eingezeichnet.
Möchtest du jetzt den Punkt P bestimmen:
Du siehst P liegt auf der roten Grade und auf der Blauen. Also genau im Schnittpunkt der Roten und der Blauen.
Weißt du wie mein den Schnittpunkt von 2 Graden bestimmt?
Zunächst brauchst du einmal beide Gradengleichungen. Diese lassen sich einfach aufstellen :
Du hast nämlich auf jeder Graden die du dort eingezeichnet hast mindestens 2 Punkte gegeben.
Bei der roten z.b: A und M2.
A ist direkt gegeben als (0|0) . M2 ist gegeben als (8|4 ) .
Stellen wir mal die Gleichung auf:
y=mx+b .
Die Steigung berechnen wir aus den beiden Punkten :
0-8 / 0-4 = 1/2 .
Also m= 1/2.
b bestimmen wir durch einen der gegeben Punkte, nehmen wir A(0|0) .Denn wenn wir die x-Koordinate von A in die Gradengleichung einsetzen,müssen wir die y-Koordinate erhalten :
0 = 1/2 0 +b .
Also ist b = 0 und wir erhalten :
y=1/2 x .
Das selbe machen wir für die Blaue Grade und setzen die Gradengleichungen dann gleich und lösen nach x auf.
(Bzw. bei P kann man es sich einfacher machen, da du weißt dass die x-Koordinate von P = M1 ist.
M1 ist ja (4/0) Also setzen wir in y=1/2x für x = 4 ein und erhalten :
y=1/2*4= 2
Also ist der Punkt : P (4|2 ).)
Q berechnen wir nach dem selben Prinzip (Schnittpunkt gelbe Grade und rote Grade).
Das ist viel Text, für wenig Arbeit.
Kurzform:
-Schau auf welchen Graden dein Punkt liegt.
- Bestimme 2 Punkte auf der Graden.
- Stelle die Gradengleichung auf.
-Setze diese Gleichungen gleich und löse nach x auf.
-Setze dein x in einer der beiden Graden ein und du erhältst deine y-Koordinate.