Straßennetz als lineares Gleichungssystem

Question

Aufgabe:

Gegeben sei das folgende Straßennetz:

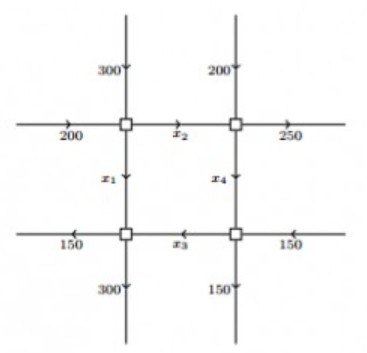
wobei die Zahlen jeweils die Anzahl der Autos angeben, die in einer Stunde die Straße passieren. Alle Straßen sollen dabei Einbahnstraßen sein, die nur in der gekennzeichneten Richtung befahren werden dürfen.

Bestimmen Sie sämtliche Werte \( x_{1}, \ldots, x_{4} \), so dass in jeder Kreuzung die Anzahl der hineinfahrenden Autos gleich der Anzahl der herausfahrenden Autos ist.

a) Formulieren Sie das Problem als lineares Gleichungssystem.

b) Bestimmen Sie alle möglichen Lösungen des linearen Gleichungssystems.

c) Wie viele Autos pro Stunde können maximal über die Strale \( x_{3} \) fahren? Begründen Sie Ihre Antwort.

Answer 1

z.B. oben links gilt  reinfahrende = rausfahrende:

300 + 200 =x1 + x2

oben rechts

200 + x2 = 250 + x4 

unt. links

x1+x3 = 150 + 300

u.re. 

x4 + 150 = x3 + 150

also insgesamt

x1   +  x2=  500

x2       - x4 = 50

x1      +x3 =   450

-x3 + x4 = 0

hat unendlich viele Lösungen, z.B. mit x4=t gibt es

x3= t       x2=50+t    und x1 =  500-t

da aber kein x negativ werden soll, muss t ≤ 500 gelten

also können wegen x3=t höchstens 500 Autos über x3 fahren.

Comments

wie kommt man darauf, dass die Lösungen unendlich sind?

Also wie rechne ich das aus?

---

Mache aus dem Gleichungssystem eine Matrix und wende den

Gauss-Algorithmus an. Es entsteht eine

Zeile mit lauter 0en.

==>  Es gibt unendlich viele Lösungen.