Berechne das Volumen der Pyramide, wenn die Angaben 8,0 dm bzw. 5,4 dm die Seitenlängen sind.

Question

Aufgabe:

Berechne das Volumen der Pyramide, wenn die Angaben 8,0 dm bzw. 5,4 dm die Seitenlängen sind.

Answer 1

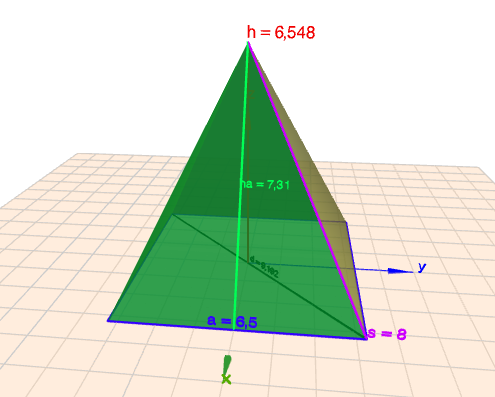
Auf dem Foto ist nur eine quadratische Pyramide zu erkennen, und zwar mit der Seite a = 6,5 und der Seitenkante s = 8,0.

Damit lauten die Ergebnisse:

Seite a (Grundseite) = 6,5
Höhe h = 6,548
Höhe a = 7,31
Seitenkante s = 8
Diagonale d = 9,192
Umfang u = 26
Grundfläche G = 42,25
Mantelfläche M = 95,031
Oberfläche O = 137,281
Volumen V = 92,216

Volumen natürlich in dm³, wenn die anderen Seite in dm angegeben sind.

Link zum Pyramiden-Rechner: https://www.matheretter.de/rechner/pyramide?a=6.5&s=8

Abbildung:



Zum Berechnen des Volumens benötigst du:
V = ¹/₃·a²·h

a ist dir gegeben, die Höhe h fehlt noch.

Wie man die Höhe aus gegebenem a und s berechnet, findest du unten auf der Seite des Pyramidenrechners:

$$ \text{Formel der Seitenkante s umstellen nach h:} \\ s = \sqrt{h^2 + \left(\frac{a^2}{2}\right)}  \quad | ()^2 \\ s^{2} = h^2 + \frac{a^2}{2}  \quad | -\frac{a^2}{2} \\ s^{2} - \frac{a^2}{2} = h^2  \quad | \sqrt{} \\ h = \sqrt{s^{2} - \frac{a^2}{2}} $$