Neu: Geozeichner 2D - Geometrische Figuren schnell und sauber zeichnen (Geometrie im Browser)

Question

Endlich bin ich dazugekommen, ein Projekt umzusetzen, das mir seit geraumer Zeit im Kopf herumschwirrt:

Dieses Programm findet man in der Assistenzrechner und es läuft direkt im Browser via HTML5. Die Mitglieder, die viele Antworten geben, werden darin einen handlichen Helfer erkennen.

Mit dem Programm lassen sich viele grundlegende geometrische Figuren schnell mit nur wenigen Angaben per Text zeichnen. Es sind implementiert:

polygon(x|y x|y …)

rechteck(x|y Breite Länge)

kreis(x|y Radius)

kreissektor(x|y Radius Startwinkel Endwinkel) - eignet sich u.a. zum Zeichnen von Winkeln


ellipse(x|y Breite Länge)

stern(x|y Radius Zacken Zackentiefe Drehung) - Polystern

Link zum Programm: Geozeichner - Geometrische Figuren in 2D zeichnen

Somit können wir die Mathematik jetzt noch sauberer darstellen. Zudem lässt sich der Link zu den erstellen Figuren einfach teilen oder man kann das Bild mit der rechten Maustaste kopieren und hier einfügen.

Comments

Geozeichner-Startseite verbessert:

---

Vorstellung im Video:

https://www.youtube.com/watch?v=nEoNU5XQ57I

---

Update 02.09.2015: - gerade als Zeichenmöglichkeit ergänzt.

Hier mal ein aktuelles Beispiel, das ich erstellt habe. Es geht um den Nachweis, dass a/sin(α) = 2·r ist.

Link zu dieser interaktiven Grafik

---

Hier ein Beispiel einer Skizze eines Dreiecks:

Einfach auf den Link zur interaktiven Grafik klicken und Elemente beliebig in ihrer Position verändern, umbenennen, Neues hinzufügen, entfernen etc.

---

Updates:

1. Animationen sind nun auch mit schrittweisen Wertänderungen via gedrückter ALT-Taste möglich! Siehe Beschreibung auf der Webseite.

2. Kleine Gallerie hinzugefügt, unten auf der Webseite.

---

Update 2017-12-07:

Ihr könnt jetzt auch die Transparenz eines geometrischen Körpers separat festlegen. Einfach hierzu eine geschweifte Klammer am Ende ansetzen mit dem Transparenzwert (zwischen 0 und 1).

Beispiel:

~draw~ ellipse(0|0 10 5){F00}{0.2};ellipse(4|3 10 5){00F}{0.3};zoom(10) ~draw~ 

~draw~ ellipse(0|0 10 5){F00}{0.2};ellipse(4|3 10 5){00F}{0.3};zoom(10) ~draw~

Link: https://www.matheretter.de/rechner/geozeichner?draw=ellipse(0%7C0%2010%205)%7BF00%7D%7B0.2%7D%0Aellipse(4%7C3%2010%205)%7B00F%7D%7B0.3%7D&scale=10

Andere Transparenz:

~draw~ ellipse(0|0 10 5){F00}{0.3};ellipse(4|3 10 5){00F}{0.7};zoom(10) ~draw~

---

Update 26.11.2021:

Man kann jetzt auch die Schriftgröße festlegen bei text und punkt. Einfach am Ende %1.5% anfügen. Also eingeschlossen in Prozentzeichen.

Beispiel:

~draw~ text(-4|0 "Text"){00F}%0.75%;text(-2|0 "Text"){0A0}%1.15%;text(0|0 "Text"){000}%1.5%;text(1.6|0 "Text"){FA9}%2.4%;punkt(4|0 "P"){F00}%2.5%;zoom(5);aus;alpha(1) ~draw~

~draw~ text(-4|0 "Text"){00F}%0.75%;text(-2|0 "Text"){0A0}%1.15%;text(0|0 "Text"){000}%1.5%;text(1.6|0 "Text"){FA9}%2.4%;punkt(4|0 "P"){F00}%2.5%;zoom(5);aus;alpha(1) ~draw~

Answer 1

Sehr schön.

Ich fände es praktisch, wenn man dort auch noch reinzeichnen und reinschreiben könnte.

Vor allem Kreise kann man im Zeichenprogramm nicht richtig platzieren.

Wo wird im Beispiel der Kreissektor eingezeichnet, den du eingegeben hast?

EDIT: kreissektor(-3|4 1 135 ,235) mit Komma zeichnet etwas.

Comments

Danke für deine Hinweise!

1. noch reinzeichnen könnte

Gekritzel mit der Maus wollen wir gerade umgehen. Vermutlich möchten einige Pfeile setzen? Ich habe gerade noch Vektoren eingebaut, diese kann man dafür verwenden: vektor(1|3 3|5)

2. und reinschreiben könnte.

Sehr gute Idee. Habe eine Textoption hinzugefügt. Eingabe per: text(-8|4 "Hier ist Text.") oder Eingabe eines Punktes mit Text: punkt(3|7 "AB")

3. Vor allem Kreise kann man im Zeichenprogramm nicht richtig platzieren.

Was klappt bei dir nicht? Ich setze einen Kreis mit x- und y-Koordinate sowie Radius, z. B. kreis(1|4 2)

4. Wo wird im Beispiel der Kreissektor eingezeichnet, den du eingegeben hast?

Siehe Dreieck, ich habe den Kreissektor für das Beispiel als Winkel-Markierung genutzt. Du kannst Kreissektoren leicht zeichnen: kreissektor(4|4 2 0 90)

---

3. Konstrutionsaufgaben sollte man nicht rechnen müssen.

Mach mal eine Skizze für die Aufgabe:

Konstruiere dem Umkreis des Dreiecks ABC mit

A(3,5), B(0,8) und C(-2,-4)

ohne, dass du die Aufgabe gleich vorrechnest.

Weg:

1. Punkte einzeichnen

2. Kreis skizzieren

3. von Hand die Eckpunkte verbinden,

4. Mittelsenkrechte einzeichnen

5. und so den gesuchten Mittelpunkt konstruieren.

---

Und wieder ein sehr guter Hinweis. Die Konstruktionsaufgabe ist in diesem Fall mit dem Geozeichner tatsächlich nicht reingeometrisch lösbar. Jedoch geht es auch sehr einfach:

Geozeichner-Link zu dieser Grafik

Durch deinen Hinweis und die Aufgabe habe ich das Programm wie folgt ergänzt:

1. Mit Raute # am Ende kann die Farbfüllung für jede Figur deaktiviert werden.

2. Für die meisten Figuren werden jetzt Fläche und Umfang ausgerechnet. Beim Polygon mit der Maus über den Umfang fahren, um die einzelnen Seitenlängen zu sehen.

3. strecke(x|y x|y) ergänzt

4. Mit Klick auf die Syntax (z. B. "ellipse(x|y Breite Länge)") wird dieser Text nun in das Eingabefeld eingefügt und man muss nur noch seine Werte einsetzen.

Vorgehen zur Konstruktionsaufgabe:

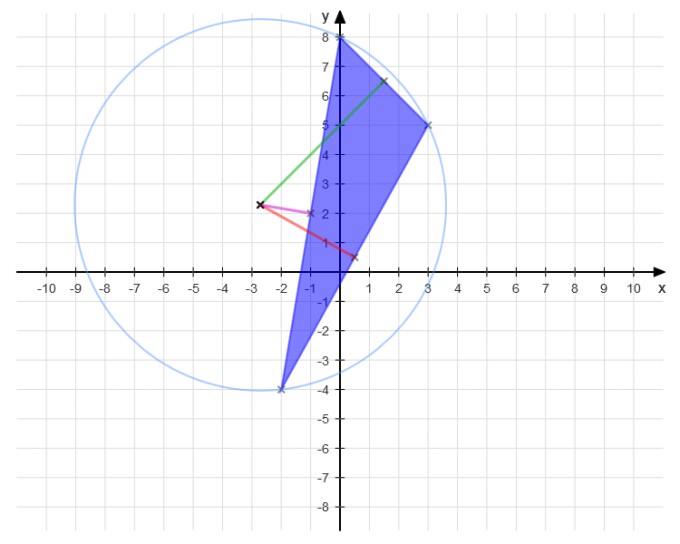
Ich habe die Dreieckspunkte als Polygon eingegeben, dann wurde mir das Dreieck mit den entsprechenden Daten angezeigt. Hier ist insbesondere der Umkreismittelpunkt U(-2,714 | 2,286) interessant. Dann musste ich nur die Koordinaten der Punkte, die auf die Mitte jeder Dreiecksseite gesetzt werden, ausrechnen und mit diesen die Strecken zum Umkreismittelpunkt setzen. Der Umkreis wurde dann mit kreis(U_x|U_y radius) gezeichnet, wobei mir auch der Umkreisradius bei den Daten angezeigt wurde.

Alles in allem sollte es jetzt noch einfacher sein, alle möglichen Geometrie-Aufgaben damit zu lösen =)

---

"Dann musste ich nur die Koordinaten der Punkte, die auf die Mitte jeder Dreiecksseite gesetzt werden, ausrechnen"

Schöne Zeichnung. Das ist frühestens in der analytischen Geometrie in dieser Form aktuell. 

In der Geometrie vorher will ich aber nichts rechnen müssen, wenn ich Konstruktionen erkläre. 

Da sollte erkennbar sein, wie man die Mittelsenkrechten konstruiert. (Kreisbogen schneiden).

Weitere häufige Konstruktionen am Dreieck:

1. Inkreis- und Inkreismittelpunkt (Braucht Konstruktion von Winkelhalbierenden.

2. Schwerpunkt.

Viele Grüsse

---

Update der Features erklärt in einem weiteren Video:

https://www.youtube.com/watch?v=u0wUOBf1Y7c

Der Schwerpunkt wird beim Polygon immer angezeigt, siehe S(x|y).

---

Du sprichst in deinem Video von HTML5. Welche weiteren Vorteile hat das?

Kann ich meine Bilder in diesem Format lokal abspeichern, vielleicht sogar bearbeiten oder muss das immer über den Link zu deinem Programm laufen?

Was, wenn die Verbindung zu deinem Programm mal nicht klappt oder du den Namen der Firma änderst?

---

Der Hauptvorteil von HTML5 ist, dass es ohne zusätzliche Software oder zusätzliches Plugin direkt im Browser läuft. Damit auf allen Geräten, auf denen moderne Browser laufen, also auch mobile Endgeräte. Das "Canvas", also die Bildfläche, auf die gezeichnet wird, ist als ein Bild direkt speicherbar, wie im Video gezeigt. Ach ja, und aus Programmierersicht: Ich muss nichts umständlich kompilieren, ich kann das Browserfenster neu laden und sehe sofort, ob mein Code klappt oder nicht. 

Ja, du kannst das Bild direkt speichern, es wird als PNG-Bilddatei gespeichert. Und ja, das PNG-Bild lässt sich nachträglich mit anderen Programmen bearbeiten.

Die Verbindung zum Programm entspricht der Verbindung zum Server. Der Server ist zu mehr als 99 % im Jahr erreichbar, keine Sorge also. Der Firmenname tut hier nichts zu Sache, ggf. meinst du die Domain, die von matheretter.de auf matheretter.de umgestellt wird. Das ist kein Problem, da alle alten Links von meinem Server automatisch umgeleitet werden.

---

Update: 

1. Vektoren-Notation geändert. Vorher: Startpunkt und Endpunkt. Neu: Startpunkt und Vektor.

2. Vektoren können nun mit Buchstaben (Labels) versehen werden.