Zeigen Sie, dass es ein x∈(1,2) gibt mit (1-2x^3)/(1-x) - (3+x^5)/(2-x) = 0.

Question

Aufgabe:

Zeigen Sie, dass es ein \( x \in(1,2) \) gibt mit

\( \frac{1-2 x^{3}}{1-x}-\frac{3+x^{5}}{2-x}=0 \)

und bestimmen Sie einen Näherungswert für ein solches \( x \), der vom wahren Wert höchstens um \( 10^{-5} \) abweicht.

Comments

Ich habe das Stichwort komplex rausgenommen, da du offensichtlich nur reelle x betrachtest.

Begründung dafür, dass eine Lösung zwischen x= 1 und x= 2 existieren muss:

(1-2x³)/(1-x) - (3+x⁵)/(2-x) = 0.

(1-2x³) / (1-x) = (3+x⁵) / (2-x)       

Ist äquivalent mit der Behauptung, dass

f(x) = (1-2x³)/(1-x)  und g(x) = (3+x⁵)/(2-x) zwischen 1 und 2 eine Schnittstelle xs haben müssen.

Du kannst die beiden gebrochenrationalen Funktionen einfach skizzieren. Einfacher Pol bei x=1 resp. x=2. Nullstellen aus Zähler ablesen. Vorzeichen überlegen.

Skizze: (Achtung: y-Richtung mit Faktor 10 gestaucht)

 

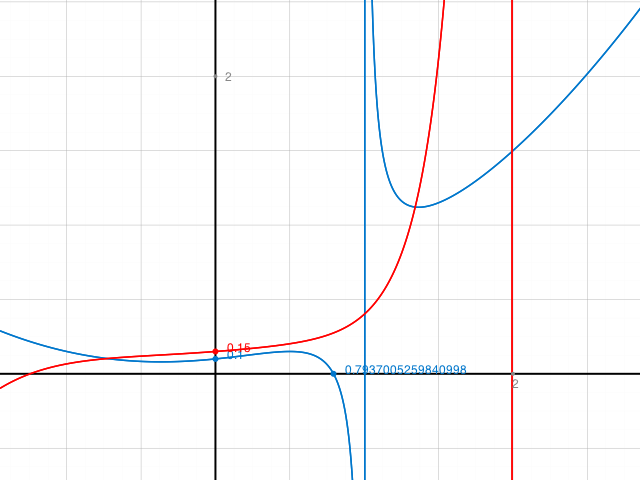
f kommt bei x=1 von + unendlich und geht dann gegen rechts wieder nach +unendlich. Kein x-Achsendurchstoss rechts von 1.

g nähert sich dem Pol x=2 von links her steigend an. verschwindet bei 2 gegen + unendlich. Die Nullstelle liegt links der y-Achse. 

Wegen der Stetigkeit beider Funktionen zwischen 1 und 2, müssen sich die beiden Kurven in diesem Bereich schneiden.

 

Answer 1

Du kannst das erstmal auf einen Hauptnenner bringen und dann reicht er dir den Zähler zu betrachten:

(1-2x^3)(2-x)-(3+x^5)(1-x)=0
2-4x^3-x+2x^4-3-x^5+3x+x^6=0
x^6-x^5+2x^4-4x^3+2x-1=0

Jetzt betrachtest du die Funktion:

f(x)=x^6-x^5+2x^4-4x^3+2x-1

und rechnest die zwei Punkte aus zwischen 1 und 2

zB f(1,1)=-1.0347und f(1,9)=23,7131

Da Funktion stetig muss eine Nullstelle dazwischen existieren.

Jetzt kannst du mit Bisektion die Genauigkeit ausrechnen:

f(1,3)<0
f(1,34)<0
f(1,342)<0
und so weiter