mir ist bei einer Differentialgleichungsaufgabe zu einer Wasseruhr etwas nicht ganz klar.
Zunächst einer paar Bilder zur Aufgabe:
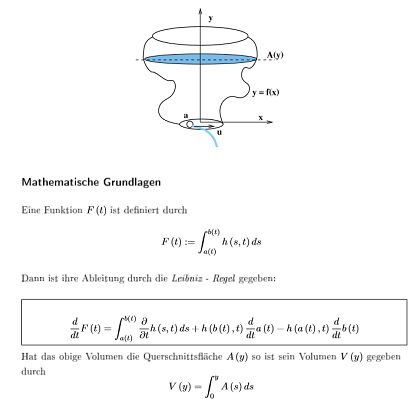


Es geht um folgendes:
In den mathematischen Grundlagen ist die Volumenfunktion abhängig von y und y ist wiederum abhängig von t also ist
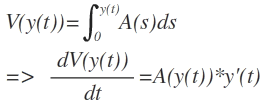
In den physikalischen Grundlagen steht unten
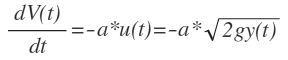
In der Lösung wird dV(t)/dt = dV(y(t))/dt gesetzt was ich intuitiv auch so gemacht habe, aber dann hab ich glaub eine Stunde lang philosophiert warum das so ist. Denn eigentlich kann ja das V(t) nicht immer gleich V(y(t)) sein außer y(t) wäre die Identität.. Ich kam zu dem Schluss dass der Prof nur zwei verschiedene Funktionen meinen kann aber diese unglücklicherweise gleich bezeichnet hat. Also V(t) = V2(y(t)). Beide Funktionen geben für beliebige t's das gleiche Volumen zurück, somit muss die Änderungsrate beider Funktionen dV(t)/dt = dV2(y(t))/dt = -a*(2gy(t))0.5 sein..
Ist da jemand anderer Meinung?
Vielen Dank schonmal..
Grüße Fraktal