lineare Gradengleichung von Excel erstellt, Kontrolle ergibt aber ganz andere Werte. Was mache ich falsch?

Question

ich habe mir von Excel aus vorhandenen X- und y-Werten  eine Grade erstellen lassen, sowie eine lineare Trendlinie. Die Gleichung lautet:

y=-0,5551x+3,1797

meine Werte sind: 

Im Idealfall sollte eine negative Steigung vorliegen.

Wenn ich nun zur Kontrolle mal einen x-Wert aus den vorhandenen nehme (zB. 5) kommt was ganz anderes raus (0,4) als der zugehörige y-Wert (2,6). Was mache ich denn nur falsch??

Comments

Warum sollte eine negative Steigung vorliegen?

Answer 1

Wenn ich eine Regression vornehme komme ich auf

f(x) = 0,6709x + 0,4353

f(5) = 3.7898

f(2.5) = 2.11255

f(1.25) = 1.273925

f(0.63) = 0.857967

f(0.31) = 0.643279

Die Frage wäre hier aber in wie weit da eine Gerade sinnvoll ist

Comments

Sag mir, wenn ich falsch liege, aber wenn ich in deine Regressionsgleichung einen meiner x-Werte einsetze (zB 5), müsste ich dann nicht meinen entsprechenden y-Wert (2,6) rausbekommen? 

---

Nein. Du siehst ja anhand der Punkte, dass es keine Gerade geben kann die genau durch alle Punkte geht. Eine Regressionsgerade ist die Gerade die die kleinsten Abweichungsquadrate erzeugt. 

Anhand der Punkte würde ich aber ohnehin nicht auf einen linearen Zusammenhang tippen. Was liegt den Punkten zugrunde ?

---

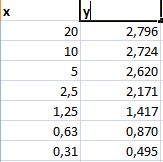
Die x-Werte entsprechen Konzentrationsangaben in ng/ml. Die y-Werte wurden durch Messung der optischen Dichte photometrisch bestimmt. Zusammen soll daraus eine Kalibriergrade bzw. Kurve erstellt werden. 

Mithilfe der Regressionsgleichung sollen dann durch Einsetzen von neuen y-Werten die entsprechenden x-Werte, also Konzentrationen, ermittelt werden. Dafür brauche ich jedoch eine Gleichung, bei der durch Einsetzen der x-Werte auch die richtigen y-Werte rauskommen.

Ich habe dies bereits mit einer polynomischen Funktion ausprobiert, die genauer gewesen wäre, bin aber am Auflösen nach x gescheitert.

Dabei habe ich weitere xy-Werte einbezogen. 

---

Eine Regression gibt dir immer nur angenäherte y-Werte, weil die entsprechenden Punkte garantiert nicht ganz genau auf einer mathematischen Funktion liegen.

Man findet natürlich ein Polynom 6. Gerades, dass durch alle diese Punkte exakt geht. Aber das nähert dann sicherlich nicht deine Funktion an.