Schnittpunkt zweier Geraden, wobei zuerst die Geradengleichung aufzustellen ist.

Question

Levje fragte nach einer Aufgabe.

Daher wäre es günstig, wenn er es zuerst probiert, bevor hier Lösungen gemacht werden.

g: 7x - 2y = 5

Wo schneiden sich die Gerade h, die parallel zu g durch den Punkt P(-3 |2) verläuft und die Gerade i, die orthogonal zu g durch den Punkt Q(-2 | 3) verläuft.

Answer 1

Okay, ich schätze, jetzt ist der Ring eröffnet :-)

Als erstes überführt man die Gleichung wieder in die Darstellung y=g(x):

7x - 2y = 5 |-7x

-2y = -7x + 5 | :(-2)

y = g(x) = 7/2 x - 5/2

 

Nun müssen zwei weitere Funktionsgleichungen aufgestellt werden:

h(x): h soll parallel zu g sein, also haben beide dieselbe Steigung. Außerdem soll sie durch den Punkt (-3|2) gehen, also gilt:

h(-3) = 2

7/2 * (-3) + n_h = 2

-21/2 + n_h = 4/2 |+21/2

n_h = 25/2

Also gilt:

h(x) = 7/2 x + 25/2

 

i(x): i soll senkrecht auf g stehen, hat also die Steigung -2/7. Außerdem soll sie durch den Punkt (-2|3) gehen, hat also die folgende Gleichung zu erfüllen:

i(-2) = 3

-2/7 * (-2)+ n_i = 3

4/7 + n_i = 21/7  |-4/7

n_i = 17/7

Also:

i(x) = -2/7 x + 17/7

 

Nun muss der Schnittpunkt bestimmt werden, also die Stelle x für die i(x) = h(x) gilt.

-2/7 x + 17/7 = 7/2 x + 25/2  |*14, um die Brüche loszuwerden

-4 x + 34 = 49x + 175  |+4x-175

-141 = 53x  |/53

x = -141/53 ≈ -2.66

i(x) = 169/53 ≈ 3.19

 

Der gesuchte Schnittpunkt ist also:

S(-141/53 | 169/53)

 

 

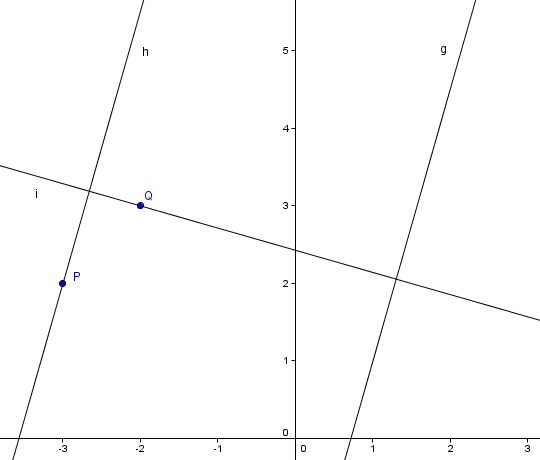
Wie wäre es, wenn du einfach mal sagst, wo es bei dir hapert?
Dann könnten wir dir vielleicht besser weiter helfen, als einfach nur das richtige Ergebnis auszurechnen.

Comments

Exzellente Lösung. Genau so hab ich es hier auch stehen.

Zum Aufstellen der Funktionsgleichungen verwende ich allerdings immer die Punkt-Steigungs-Form. Leider wird das aber in den meisten Schulen so nicht gelehrt. Dabei finde ich den Weg etwas einfacher.

Also: h soll parallel zu g sein, also haben beide dieselbe Steigung (7/2). Außerdem soll sie durch den Punkt (-3|2) gehen, also gilt:

h(x) = 7/2 * (x + 3) + 2 = 7/2x + 21/2 + 2 = 7/2x + 25/2

 

---

Hab ich bis vor kurzem im Forum hier auch noch benutzt, allerdings steht sie seit G8 soweit ich weiß allgemein nirgendwo mehr im Rahmenplan.

Deshalb mach ich immer lieber den Ansatz mit dem bekannten Punkt, auch deshalb, weil es später für Rekonstruktionsaufgaben sehr hilfreich ist, wenn man das Prinzip schon häufiger verwendet hab.

 

Ich selbst benutze aber natürlich auch Punkt-Punkt- bzw. Punkt-Steigungs-Form, wenn ich denn mal in die Verlegenheit gerate, eine lineare Funktion aufstellen zu müssen ;-)