Rohrlänge mit Kurven/Bogen berechnen

Question

Aufgabe:

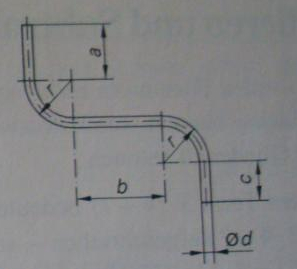
Berechnen Sie die Rohrlänge \( l \) des Rohres:
a) mithilfe von Variablen,
b) für \( a=140 \mathrm{mm} \\ b=225 \mathrm{mm} \\ c=103 \mathrm{mm} \\ r=120 \mathrm{mm} \\ d=12 \mathrm{mm} \varnothing \)

Ansatz:

Ich ging bei den Kurven bzw. Bögen von zwei Viertelkreisen aus, also den Umfang von zwei Viertelkreise nbzw. einem Halbkreis. Folgendes kam dabei heraus nach dem ich meine erdachte Formal dazu durch Maxima gejagt habe (ein CAS auf Linux):

\( l=\pi(r-d)+c+b+a \)
\( l=900 m m \)

Da sowas in der Art für mich neu ist wollte ich jedoch nun wissen ob meine Annahme richtig ist.

Comments

Allein durch das multiplizieren mit π kann das Ergebnis nicht so glatt sein,⇒844,99mm.

Answer 1

  ich denke nicht das in der Praxis so gerechnet wird. Das verwendete Rohr dürfte die
Länge

  l = a + 2*π*r/4 ( Viertelkreis ) + b + 2*π*r/4 ( Viertelkreis ) + c
  l = a + b + c  + π*r

  haben.

  b.)

  l = 140 + 225 + 103 + 120 * π
  l = 844.99

  mfg Georg

  Bei Fehlern oder Fragen wieder melden.

Comments

Okay klar.. mein Fehler.. hatte den Durchmesser vom Radius r abgezogen was ja unsinnig ist.. danke :)

---

Ist zwar schon eine Weile her, allerdings müsste die Hälfte des Rohrdurchmessers von der Rohrkrümmung r subtrahiert werden. Der jeweils äußere Teil des Rohres wird gestreckt, der innere gestaucht, sodass sich folgendes ergibt:

l= a + (r-d/2)*π/2 + b + (r-d/2)*π/2 + c

l=a + b + c + (r-d/2)*π

l=140 + 225 + 103 + (120-12/2)*π

l=826,14mm

---

Ich denke diese Frage kann nur aus der Praxis / Erfahrungen
beantwortet werden.
Wird ein Rohr beim Biegen tatsächlich gestaucht bzw. gestreckt ?
Eine Stauchung kann ich mir noch vorstellen. Eine Streckung
weniger.