Ich habe in Excel einen Graphen zeichnen lassen anhand der X und Y Werte. Wie kann ich die Funktionsgleichung anzeigen?

Question

Ich habe in Excel eine Gleichung zeichnen lassen anhand der X und Y Werte. Besteht jetzt die Möglichkeit, dass ich die Funktionsgleichung des Graphen angezeigt bekomme? wenn ja wie ?

danke schonmal

Comments

Ich vermute dass es dazu keine einfache schöne Funktionsgleichung gibt.

Je nach Anwendung würde ich hier über eine Regression nähern.

Die x-Koordinate von J wurde angepasst, weil sonst die x-Koordinaten von I und J gleich wären.

~plot~ {1|15};{1,5|12};{2|10};{3|8};{7|6};{10|5};{14|4,5};{18|4,25};{22|4};{25|3,75};{28|3,5};{32|3,25};{38|3};{42|2,75};{48|2,5};{52|2,25};{58|2};{62|1,75};[[-1|65|-1|16]] ~plot~

---

ja genau der punkt J sollte (28/3,75) heißen

Regression.. hm das ist aber lang her seit dem ich das gemacht habe :D

könntest du mir dabei helfen ?

---

(28/3,75) kann nicht sein weil sonst die x-Koordinate von J mit der von K übereinstimmen würde.

Für eine Regression braucht man eine Funktionsvermutung. Diese ergibt sich aus dem Sachzusammenhang. Was stellen die Koordinaten im Sachzusammenhang dar ?

Du kannst auch abschnittsweise Funktionsterme finden. Auch das ergibt sich aus dem Sachzusammenhang.

---

Punkt A zum Beispiel bedeutet:

bei einem einkaufspreis von 1 euro ist der verkaufsfaktor 15.

Das heißt dass wir das Teil für 1*15= 15 Euro verkaufen.

und so weiter.

Meine vermutung war: f(x) = a * e ^{b*x}

abschnittsweise.. ja das wäre auch eine möglichkeit aber trotzdem komme ich nicht drauf wenn ich nur den graphen habe..

 

Answer 1

Ich vermute, dass Du einen Graph der Wertepaare (Stützstellen) zeichnen lassen hast und nun eine

explizite Formel dazu bekommen möchtest...

Da es mehrere Algorithmen dazu gibt, bräuchten wir mehr Randbedingungen.

a) lineares Verbinden der Stützstellen (exaktes Verbinden der Stützstellen; sieht jedoch unschön aus)

b) Regression (meist nichtlinear) -> hier toleriert man das nicht exakte Übereinstimmen der Stützstellen mit der Näherungsformel

c) Spline Interpolation: abschnittsweise werden die Stützstellen weich verbunden: meist kubisch, also per Polynom Grad 3

d) Interpolationspolynom: aus den vorgegebenen Stützstellen wird ein exaktes Polynom berechnet, dass durch alle Punkte läuft. Je mehr Punkte, um so größer wird der Grad und so höher auch das Überschwingen an den Rändern. Daher nur bis Grad 7 sinnvoll -> absolut nicht für physikalische Messreihen geeignet

dafür aber für Zahlenfolgen

Oder geht es Dir nur um das Sichtbarmachen der Formel, die Du bereits eingegeben hast?

Erst mit mehr Fakten können wir genauer antworten.

Comments

danke schonmal für die antwort. 
also ich habe davon nicht viel verstanden aber ich versuche es dir nochmal genauer zu erkären. 
ich habe die punkte A(1/15) B(1,5/12) C(2/10) D(3/8) E(7/6) F(10/5) G(14/4,5) H(18/4,25) I(22/4) J(22/3,75) K(28/3,5) L(32/3,25) M(38/3) N(42/2,75) O(48/2,5) P(52(2,25) Q(58/2) und R(62/1,75) Verlauft von links oben nach rechts unten.
nur damit du dir die Kurve vorstellen kannst :D 
diese Kurve sieht für mich wie eine E-Funktion aus. Da ich die Punkte habe kann ich Sie einzeichnen (auf papier oder auf Excel) 
Jetzt hätte ich gern die Funktionsgleichung davon. Ob mathematisch aufgestellt oder auf Excel ist mir egal. Hauptsache ich habe die Gleichung dieser Funktion

---

Endlich mal schöne Stützstellen:

a) lineares Verbinden

aB=Array(1,1.5,2,3,7,10,14,18,22,24,28,32,38,42,48,52,58,62);

aC=Array(15,12,10,8,6,5,4.5,4.25,4,3.75,3.5,3.25,3,2.75,2.5,2.25,2,1.75);

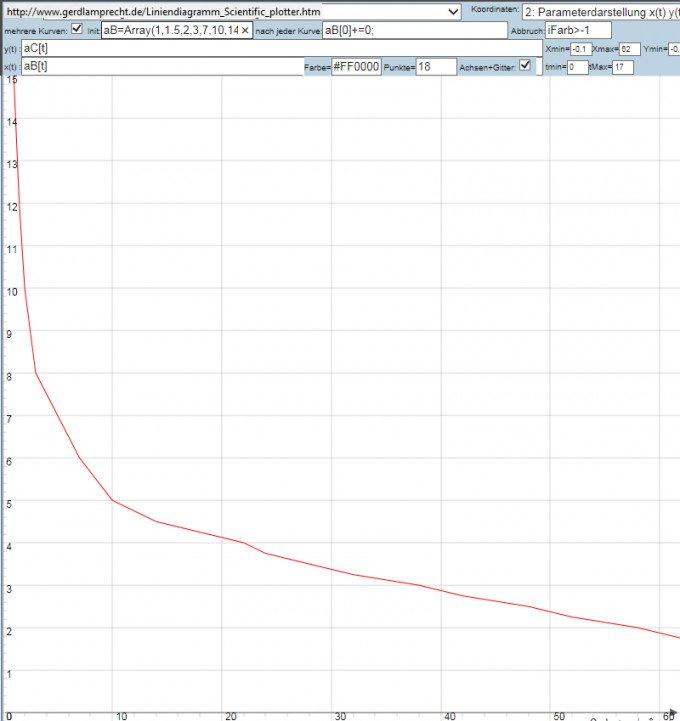
b) nichtlineare Regression mit 4 Parameter ergibt

-4.395019119e-2*x+4.308172354+12.59709369/x-1.818476383/pow(x,2)

im EXCEL Syntax: -0,04395019119*x+4,308172354+12,59709369/x-1,818476383/x^2

Der Iterationsrechner zeigt die minimalen Abweichungen gegenüber dem Idealfall: nur die 1. Nachkommastelle schwankt minimal

http://www.gerdlamprecht.de/Roemisch_JAVA.htm#-4.395019119e-2*x+4.308172354+12.59709369/x-1.818476383/@Px,2)@NaB=Array(1,1.5,2,3,7,10,14,18,22,24,28,32,38,42,48,52,58,62);aC=Array(15,12,10,8,6,5,4.5,4.25,4,3.75,3.5,3.25,3,2.75,2.5,2.25,2,1.75);@NaD[i]=Fx(@Bi]);@Ni%3E17@N0@N0@N#

zum Vergleich die "Trendlinie" von EXCEL: sie kennt nur 4 einfache Regressionstypen:

exponentiell:

potentiell:

zu den Funktionstypen c und d) mehr im nächsten Kommentar ...

---

d) Interpolationspolynom:

hier haben die exakten Stützstellenpunkte oberste Priorität, während die Zwischenwerte egal sind. Da bei 18 Stützstellen ein Polynom Grad (Stützstellen -1)=17 herauskommt,

ergibt sich ein extremes Überschwingen zu den Rändern hin:

1.67874838246307995987178e-20*pow(x,17)-7.796703337686185813574342783e-18*pow(x,16)+1.650026811342015253637415669e-15*pow(x,15)-2.1082807493227529267332e-13*pow(x,14)+1.8165787723448847219546745193e-11*pow(x,13)-1.11660457996026929413234e-9*pow(x,12)+5.0512500945720827053870872766e-8*pow(x,11)-1.710150653708562417386776627e-6*pow(x,10)+0.0000436338574377289756899842*pow(x,9)-0.000838229672899359704615972*pow(x,8)+0.0120233241471165075043447899*pow(x,7)-0.12665960943435422465083933*pow(x,6)+0.9540382852682293431365668*pow(x,5)-4.9291232435421403137488889175*pow(x,4)+16.3571289603768498421916323387*pow(x,3)-31.09493751593917797604888136147*pow(x,2)+25.792267040245291362897985*x+7.036059015430447830353454

Wie bereits gesagt: für physikalische Messreihen und Vorhersagen für den weiteren Verlauf absolut ungeeignet.Außerdem kann EXCEL nicht mit so langen Formeln arbeiten.
c) Spline Interpolation: Stützstellen werden exakt getroffen und das Überschwingen wird minimiert, indem Abschnittsweise nur ein Polynom 3. Grades die Teilstücke "weich" verbindet.Bei EXCEL nennt sich das "Punkt (X Y) interpolierte Linien":
Nachteile:- keine Tendenz für den weiteren Verlauf möglich (keine Vorhersage für x> 62 )- kein Bezug zur physikalischen Wirklichkeit- Ausreißer (kleine Messfehler) werden exakt getroffen und machen die weiche Kurve an diesen Stellen wellig
Noch was zu b)Da die Stützstellen bei x=62 aufhören, kann man keine genaue Tendenz für den weiteren Verlauf vorhersagenEs kann durchaus sein, dass ein exponentieller Abfall (jedoch mit mehr als den 3 Parametern von EXCEL) vorliegt, und die von mir für x <=62 optimierte Kurve dann für x>62 ungenauer wird, als eine mit 4 oder 5 Parameter Exponentialfunktion...
Gibt es grobe Schätzungen, wo der y-Wert liegt, wenn x viel größer wie z.B.:100  {mein Vorschlag zu b) ergibt dort 0.038942324261699336}1000 { mein Vorschlag zu b) ergibt dort -39.62942 }10000 ?
Deshalb hier noch eine weitere Kurve mit 4 Parametern, die für große x gegen 1 konvergiert:(x+0.8978860149)/(0.01158953574*x*x+0.1463622031*x-0.02362042382)+1

http://www.gerdlamprecht.de/Roemisch_JAVA.htm#(x+0.8978860149)/(0.01158953574*x*x+0.1463622031*x-0.02362042382)+1@NaB=Array(1,1.5,2,3,7,10,14,18,22,24,28,32,38,42,48,52,58,62,100,1e3,1e4);aC=Array(15,12,10,8,6,5,4.5,4.25,4,3.75,3.5,3.25,3,2.75,2.5,2.25,2,1.75,1.74,1.085,1.008);@NaD[i]=Fx(@Bi]);@Ni%3E20@N0@N0@N#

fast ganau so genau wie mein 1. Vorschlag zu b)und per http://www.gerdlamprecht.de/Liniendiagramm_Scientific_plotter.htm

---

Noch was zu 3-Parameter Regression: a*e^{b*x}, die gegen 0 konvergiert

ergibt 10.51416646e^{-3.398706015e-2*x}

EXEL: 10,51416646*exp(-0,03398706015*x)

ABER nur ab x>20 zu gebrauchen!

bei x=1 ist der Funktionswert um  4.837 Einheiten zu klein!

Besser 4-Parameter:

(x+1.688390638)/(5.02870859e-3*x*x+1.744854379e-1*x-1.262511534e-3)

EXCEL: (x+1,688390638)/(0,00502870859*x*x+0,1744854379*x-0,001262511534)

fast immer stimmt die 1. Nachkommastelle

---

noch was zur vermuteten e-Funktion:

um sie für Deine Stützstellen noch besser zu optimieren, sind 2 Fakten wichtig:

§1: Was soll bei x= 1/2 = 0.5 herauskommen?

§2: 4-Parameter nichtlineare Regression vom Typ:

f(x) = f₁(x) * e^[f₂(x)]+f₃(x)

wenn sie gegen 0 konvergiert, ist f₃(x)=0

Mit nur 2 Parametern {a, b} hat man immer Bereiche starker Abweichung (entweder vorn x<10 oder Mitte x= 16 ... 40 )