Modell eines regelmäßigen dreiseitigen Prismas

Question

Aus 144 cm Draht soll ein Modell eines regelmäßigen dreiseitigen Prismas hergestellt werden,bei dem sämtliche Kanten gleich lang sind. Berechne Volumen und Oberflächeninhalt des Körpermodells.

Answer 1

 

ein dreiseitiges Prisma  hat dann 9 Kanten der Länge a:

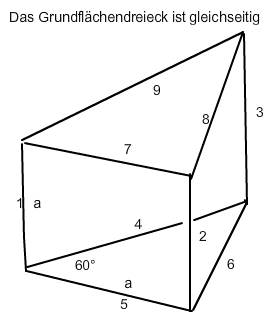
144 cm : 9 = 16 cm = a

A_Δ =  a² /4 * √3    ≈ 110,85 cm²     

    ( Fläche gleichseitiges Dreieck = 1/2 * a² * sin(60°) )

Volumen = A_Δ * a  ≈  1733,62 cm³    ( V = Grundfläche * Höhe)

Oberfläche = 2*A_Δ + 3* a² ≈ 989,7 cm²

Gruß Wolfgang

Answer 2

144/9 = 16

V = 1/2·16^2·SIN(60°)·16 = 1774 cm³

O = 16^2·SIN(60°) + 3·16·16 = 989.7 cm²

Answer 3

Ein dreiseitiges Prisma hat 9 Kanten. Also 144:9 = 16. Alle Kanten sind 16 cm lang. Die Grundfläche des Prismas ist ein gleichseitiges Dreieck und hat die Fläche 16²·√3/4 = 64·√3. Das Volumen des Prismas ist 64·√3·16 = 1024·√3.

Die Oberfläche hesteht aus zwei Dreiecken (s.o.) mit einer Fläche von 128·√3  sowie 3 Quadraten (3·16² = 768), zusammen also 128·√3 + 768.