Deltoid 2 Seiten u. Fläche gegeben wie rechnet man die Winkeln aus?

Question

Hi,

bin schon lange am suchen, finde aber nichts, kann mir wer bei folgender Aufgabe helfen?

Von einem Deltoid kennt man die Längen zweier Seiten, die 8 und 15 Einheiten
betragen, sowie den Flächeninhalt, der 120 Quadrateinheiten beträgt. Man berechne die
vier Winkel des Deltoids.

Liegt der Inkreisradius im rechten Winkel zur seite a? dann könnte man sich e/2 ausrechnen und dann f und dann die WInkel oder?

mfg

Comments

Folgendes ist dir bestimmt bekannt:

Die beiden Diagonalen schneiden sich in einem rechten Winkel.

Benutze, dass (ef)/2 = 120 .

Zudem hast du 4 rechtwinklige Teildreiecke im Deltoid mit einer Kathete der Länge e/2. (Falls ihr irgendwo festgelegt habt, das f die Spiegelungsachse ist). Ansonsten halt 2 Fälle rechnen.

---

kannst du das noch etwas mehr ausführen?

Versteh nicht wie ich da auf e bzw. f kommen soll, ich hab bei den teildreiecken ja nur eine Seite gegeben und die Fläche bringt mir ja auch nichts, da ich sie nicht einfach viertel kann.

Answer 1

Deltoid = Drachenviereck:

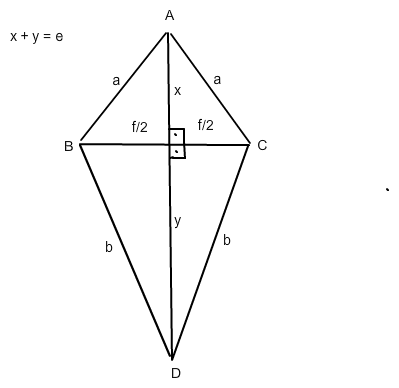
\(\overline{BC}\) =  \(\overline{f}\) 

\(\overline{AD}\) =  \(\overline{e}\)   ,    e = x + y 

Der Flächeninhalt  beträgt    A =  1/2 * e * f = 120

Die Diagonalen stehen senkrecht aufeinander und e halbiert f  im Punkt S :

Pythagoras →   x² + (f/2)² = b²   und  y² + (f/2)² = a²        ( a = 8, b = 15 )

Die Lösung des Gleichungssystems aus 4 Gleichungen mit 4 Unbekannten ist "von Hand" lästig.

....

Es ergibt sich (für positive Unbekannte eindeutig):

x = 225/17 ;  y = 64/17 ;  e = 17 ;  f = 240/17      (Rechnerlösung)

Dann kannst du alle Winkel in den Teildreiecken mit Pythagoras und dann alle gesuchten Winkel einfach durch Addition ausrechnen.

Gruß Wolfgang

Comments

Die Lösung des Gleichungssystems aus 4 Gleichungen mit 4 Unbekannten ist "von Hand" lästig.

Dann mach es doch anders (es ist ziemlich trivial).

---

Kann durchaus sein. Mach es doch einfach.

Answer 2

Der Deltoid ist ein spezieller Drachen (Wikipedia). Seine Darstellung ist ein gleichseitiges Dreieck ABC (Schenkellänge 15), dem ein anderes gleichseitiges Dreieck ABD  (Schenkellänge 8) mit der gleichen Basis x=AB entnommen wurde. Seine Symmetrieachse geht durch C und D und schneidet AB in H. Sei h₁ = HC und h₂=HD. Dann berechnet sich seine Fläche (hier F=120) als F=h₁·x/2 - h₂·x/2. h₁ und h₂ lassen sich mittels Pythagoras durch x ausdrücken und dann lässt sich x bestimmen. Schließlich lassen sich alle Winkel des Deltoides mit Hilfe von Winkelfunktionen bestimmen.  

Comments

sorry aber damit kann ich absolut nichts anfange, kannst du das einfacher erklären?

---

Als erstes solltes du dir eine genaue Vorstellung davon verschaffen, wie ein Deltoid aussieht (Wikipedia). Dann solltest du ein Deltoid selbst konstruieren mit den Seitenlängen 15 und  8 sowie einer selbstgewählten Diagonalenlänge. Dann beschriftest du  die Ecken des Deltoid mit A, B, C und D, sodass eine Diagonale (außerhalb der Deltoidfläche) AB und die andere Diagonale CD heißt. Wenn du dir jetzt meinen Text durchliest und dabei deine Skizze anschaust, könnest du den Text verstehen. Wenn nicht, stell weiterhin gezielte Fragen.

---

> Seine Darstellung ist ein gleichseitiges Dreieck ABC (Schenkellänge 15), dem ein anderes gleichseitiges Dreieck ABD  (Schenkellänge 8) mit der gleichen Basis x=AB entnommen wurde.

Wie soll das gehen?

Du meinst so etwas: (gleichschenklige Dreiecke)

> Der Deltoid ist ein spezieller Drachen (Wikipedia).

Nach Wikipedia bezeichnet man auch "normale" Drachen als Deltoide  (konkav bzw. konvex)

https://de.wikipedia.org/wiki/Drachenviereck

---

Du hast natürlich recht. Damit habe ich den Fragesteller nur verwirrt.

---

ja stimmt^^

werds mir gleich mal genauer anschauen, um es zu verstehen.

---

Die gegebenen Maße lassen ein konkaves (eigebeultes) Deltoid wie von Roland angenommen gar nicht zu.
Es ergibt sich vielmehr zwingend ein konvexes Drachenviereck.

---

Irgendwie komm ich nicht ganz hin, x kann ja nicht negativ sein...

Das ist die Lösung eines kollegens, hab ich leider nicht ganz verstanden, am schluss war auch leider keine Zeit mehr um fragen zu stelllen. kann das vielleicht einer von euch erklären?