Hi,
wenn wir uns ein Beispiel herannehmen:
f(x)=1/x
f(x) mal noch visualisiert.
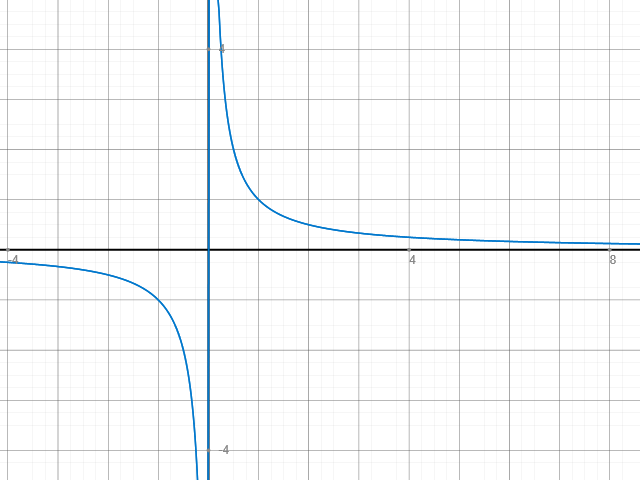
Wenn wir nun den Grenzwert/Limes berechnen wollen für x->∞, uns also anschauen wollen, was mit dem Graphen im Unendlichen passiert, dann schreiben wir das erstmal als:
limx->∞ f(x) = limx->∞1/x = 0
D.h. aus obiger "Rechnung" erkennen wir, dass im Bereich für x->∞ der Graph sich der 0 annähert. Genau das sieht man auch im Schaubild. Wir nähern uns der x-Achse an, erreichen sie aber nie.
Speziell unserem Falle mit f(x)=1/x ist auch die Stelle 0 sehr interessant. Die Stelle x=0 ist nicht definiert (es darf nicht durch 0 geteilt werden), dennoch möchte man eine Aussage machen, was ein wenig rechts und ein wenig links davon passiert.
Im Schaubild ist diese Antwort leicht zu beantworten. "Ein wenig rechts" davon, oder mathematisch x->0+ strebt unser Graph gegen +∞. "Ein wenig links von 0", oder wieder mathematisch ausgedrückt x->0-, streben wir im Gegenzug nach -∞.
In der Limesschreibweise ist dies dann:
limx->0+ 1/x = ∞ (für den ersten Fall)
Der Limes ist also eine Schreibweise um eine "Umgebung" (also "nahe etwas") zu beschreiben.
Alles klar?
Grüße