Wie lange bräuchte ein Heissluftballon einmal um die Erde, wenn ...

Question

Die Frage lautet: Wie lange bräuchte ein Heissluftballon für einmal um die Erde, wenn er 40° Nord ist und ein Westwind mit 15 m s-1 weht?

Answer 1

Die Zeit berechnet sich aus der zurückgelegten Strecke s durch die Geschwindigkeit v. Die Strecke s ist in diesem Fall ein Kreis, der sich bei 40° nördlicher Breite um die Erde schlingt. Wie folgende Skizze zeigt ist der Radius r dieses Kreise \(r=R\cdot \cos{40°}\), wenn \(R\) der mittlere Erdradius ist.

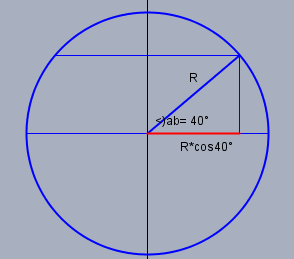
Daraus folgt $$s=2\pi \cdot r=2\pi \cdot R \cdot \cos{40°}\approx 2\pi \cdot 6371\text{km} \cdot 0,76604 \approx  30664,9\text{km}$$ Die benötigte Zeit t für diese Strecke ist dann $$t=\frac{s}{v}\approx\frac{30664,9\text{km}}{15\frac{\text{m}}{\text{s}}}\approx 2,0443\cdot10^6\text{s}\approx 567,87\text{h} \approx23,7 \text{d} $$ nach knapp 3 Wochen und 3 Tagen ist der Ballon einmal rum.

Gruß Werner

Comments

Vielen Dank, das haben Sie sehr gut erklärt, so dass es auch für mich als Mathematik-Banause gut verständlich ist!