Maße bei einem rechtwinkligen Dreieck

Question

Können diese Maße für ein Zelt exakt sein? Prüfe rechnerisch. Kann mair da jemand helfen? Sophie

Answer 1

Hi,

wenn wir die Schräge von 1,20 m überprüfen wollen nehmen wir die Front und teilen dies in zwei rechtwinklige Dreiecke. Die eine Kathete entspricht der Höhe mit 1m. Die andere Kathete ist 1,30m/2 = 0,65m lang.


Pythagoras:

0,65^2+1^2 = x^2 = 1,4225

x = √1,4225 = 1,19


Im Rahmen der Genauigkeit hätte ich also gegen diese Maße nichts einzuwenden. Exakt wie verlangt sind sie allerdings nicht.

Grüße

Comments

Noch eine Zeichnung.

 

Die Frontansicht. Als bekannt angenommen werden die Höhe mit 1m und die Basis mit 1,3 m. Rechtwinkliges Dreieck wird gesucht, damit man Pythagoras anwenden kann und überprüfen kann, ob x=1,2.

Für den Pythagoras und die Schlussfolgerung siehe Antwort.

Answer 2

Ich mache mal eine Skizze

Wenn wir also die untere Länge und die Höhe als exakt annehmen kann die Hypotenuse nicht exakt sein.

Die Maße des Zeltes sind also nicht exakt angegeben.

Answer 3

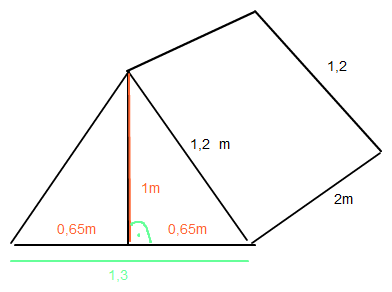
Eigentlich kann man hier nur die Höhe des Zeltes und die Seitenlänge des Zeltdaches überprüfen.

Die Grundfläche ist ein Rechteck mit den Maßen 1,3m und 2m und stimmen so gesehen.

Der Zelteingang ist ein gleichschenkliges Dreieck.dann gilt  a²+b²=c²

a=1m  b=0,65m   c sollte 1,20 sein

c= √(1²+0,65²)=1,192      ≈ 1,2m

um die Höhe zu  überprüfen stellt man den Pythagoras um

b=0,65   c=1,2    a ist gesucht

a=√(1,2²-0,65²) =1,00872≈ 1m

Die  angegbenen Maße stimmen also.

Comments

Meiner Meinung nach lässt sich das ganze vereinfacht ausrechnen:

a^2+b^2=c^2     |-a^2

b^2=c^2-a^2

b^2=1,22^2-1^2

b=0,6633249581m > b=0,65m

Also sind die Maße nicht korrekt.