Komplexe Zahlen. Gleichung lösen und grafisch darstellen: Bsp. x^3 - 8 = 0

Question

wie löse ich so eine komplexe Gleichung, bitte mit ausführlichen lösungsweg zum nachvollziehen!

Answer 1

$$ (1+j )\cdot z^5- 2 \sqrt{2}=0 $$
$$ (1+j )\cdot z^5= 2 \sqrt{2} $$
$$  z^5=  \frac{2 \cdot \sqrt{2}}{1+j}$$
$$  z^5=  \frac{2 \cdot \sqrt{2}}{1+j} \cdot \frac{1-j}{1-j}$$
dritte binomische im Nenner !
$$  z^5=  \frac{2 \cdot \sqrt{2}}{1+1} \cdot (1-j)$$
$$  z^5=   \sqrt{2} \cdot (1-j)$$
cartesisch zu euler
$$  z^5=   \sqrt{2} \cdot e^{-j\frac \pi 4}$$
$$  z=   2^\frac1{10} \cdot e^{-j\frac \pi {20}}$$
Achtung - das ist nur der Grundwert - es gibt noch 4 weitere Ergebnisse!

Comments

oh man, das klingt ziemlich komplex. danke dir erstmal. hab überhaupt keinen richtigen Ansatz für  die aufgaben!

Answer 2

Aufgabe a)

                                          

Comments

DANKE Dir, hast noch eine Idee zu den anderen aufgaben? b.) oder c.)

---

wie soll ich so eine Funktion den komplex grafisch darstellen, verstehe das nicht. einfach normal Zeichen?

---

Das kannst Du in der Gaußschen Zahlenebene darstellen:

---

cool danke. bei b.) hab ich substituiert mit x³ und komme auch x= 4... kann das hinkommen

---

wie soll ich den für aufgabe noch Lösungen in der komplexen zahlenebene ermitteln

Answer 3

Hallo dtfahrer,

b) z⁶ = - 64 

Habe das irgendwann mal allgemeiner aufgeschrieben und auf deinen Fall angepasst.

 Lösung der komplexen Gleichung  zⁿ = w     [ n ∈ ℕ , n ≥ 2 ]

                                                             z⁶ = - 64      [ n = 6 ]

w hat dann eine der Formen  w  =  a + i · b  = r · e^i ·φ  =  r · ( cos(φ) + i · sin(φ) )  [ oder w muss in eine solche umgerechnet werden ].

                                          a = - 64 , b = 0

Den Betrag  |w| = r  und das Argument φ_w  kann man dann direkt ablesen oder aus folgenden Formeln berechnen:

r = √(a² +b²) und  φ_w = arccos(a/r) wenn b≥0    [  - arccos(a/r) wenn b<0 ] .

  r = 64  und  φ_w = arccos(-64/64) = arccos(-1)  = π   [ = 180° ]

Die n Werte z_k  für z = ⁿ√w  erhält man mit der Indizierung k = 0,1, ... , n-1

aus der Formel    z_k = ⁿ√r · [ cos( (φ_w + k · 2π) / n ) + i · sin( (φ_w + k · 2π) / n ) ] 

                                    = 2 · [ cos( (π + k · 2π) / 6 ) + i · sin( (π + k · 2π) / 6 ) ]

z = ± 2i  oder  z = √3 ± i  oder z = - √3 ± i  

(die x-Werte sind nicht nummeriert, weil mein Rechner die Lösungen nicht in der Reihenfolge angibt, in der man sie gemäß Anleitung errechnet.) 

[ Die Eulersche Form ist  jeweils  z_k =  ⁿ√r · e^{i·(φw+k·2π)/n} ]

----------------

Wenn du dann zeichnen musst:

Für z_k = a_k + b_k·i jeweils den Punkt (a_k | b_k)  in der komplexen Ebene eintragen und den Pfeil vom Nullpunkt aus dorthin zeichnen. (Die Pfeilspitzen liegen alle auf einem Kreis um den Ursprung.

Zum Beispiel  z = √3 + i :

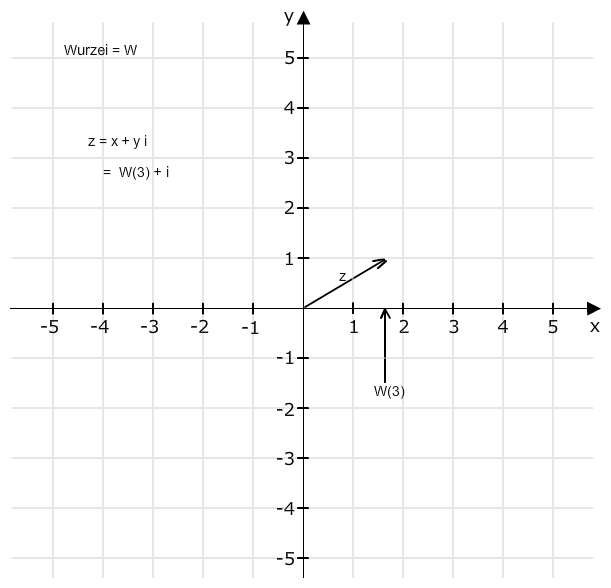
Alle weiteren Lösungen ergeben sich, wenn man den Pfeil z 6-mal jeweils um 360/n = 60° gegen den Uhrzeigersinn um den Nullpunkt dreht.

Gruß Wolfgang

Comments

danke dir, wie verhält sich das mit a.)

---

z³ = 8 ,  n = 3

w = 8 + i * 0  →  a = 8 , b = 0

→  r = 8   und  φ_w = arccos(8/8) = arccos(1) = 0 

(wenn man Ahnung von der komplexen Ebene hat, ist das natürlich auch sofort klar. Interessanter ist die allgemeine Anleitung, wenn bei w der Imaginärteil b nicht = 0 ist. Rechnet sich aber genauso)

usw.

Lösungen:

 x = 2  oder   x = -1 ± √3  

---

bin gerade bei d.) bei und bei e.) komme ich gar nicht mehr zu recht.Hast du da einen ansatz

---

kannst mir mal für b) sagen wie das aussehen soll? die a=-64 und b= 0 ud das abtragen vom Nullpunkt?

---

d) hab ich rausbekommen. e.) wäre noch interessant, da muss ich passen. mit dem einzeichnen weiss ich nicht so recht. wie ich das abtragen muss

---

Ausgehend von  z⁵ = √2 - √2 * i   (Pleindespoir)

erhältst du gemäß meiner Anleitung mit a = √2 und b = - √2

die Lösungen

x ≈ -1.023497728 - 0.5214981402·i

 x ≈ 1.134555972 - 0.1796960126·i

 x ≈ 0.1796960126 - 1.134555972·i

 x ≈ 0.5214981402 + 1.023497728·i

 x ≈ - 0.8122523963 + 0.8122523963·i

(die x-Werte sind nicht nummeriert, weil mein Rechner die Lösungen nicht in der Reihenfolge angibt, in der man sie gemäß Anleitung errechnet.)

Jetzt  kannst  du z.B. wie in meinem Bild für

x = -1.023497728 - 0.5214981402·i  ≈  -1,02 - 0,52 i

den Punkt P( -1,02 | - 0,52)  einzeichnen.

Die anderen Punkte brauchst du nicht unbedingt, denn du kannst jetzt einen Kreis um den Ursprung zeichnen und dann den Winkel 360°/5 = 72° beginnend beim Schenkel  OP 5-mal antragen und erhältst  alle Pfeilrichtungen (gleiche Pfeillänge)

---

ich kann mir das schlecht vorstellen mit dem zeichnen wie müsst ich denn z.b a.) oder b.) einzeichnen?  ich habe das in psi Winkel ausgerechnet, anders wie du das gemacht hast.

---

oder brauch ich einfach nur a und b schauen auf dem koordinatensystem und abtragen?

---

du wirst doch einen Punkt  (a,b) ≈ (-1 | -0,5)  in das Koordinatensystem in meinem Bild eintragen können.

Für den Punkt (1 | √3) aus b) findest du ein Bild in der Antwort.

---

ach so ist das gemeint. na klar bekommen ich das hin;) sorry, brauchte nur einen gedankenanstoss!!;)

vielen dank nochmal für die ausführlichen Erklärungen.