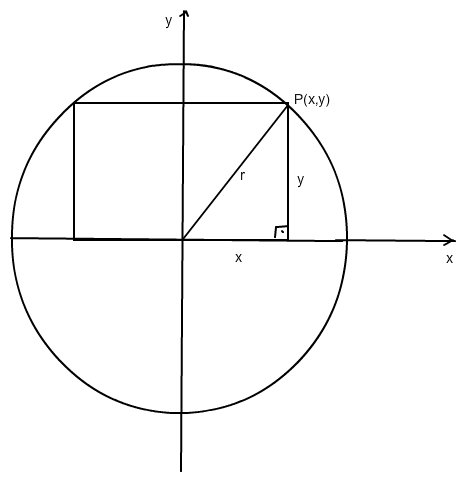
Für den Flächeninhalt gilt A(x,y) = 2x * y mit y = √(r2 - x2) nach Pythagoras
y einsetzen → A(x) = 2x * √(r2 - x2)
um das Maximum von A zu bestimmen, leitet man ab und setzt A '(x) = 0
A '(x) = 2·√(r2 - x2) - 2·x2 / √(r2 - x2) = (2r2 - 4x2) / √(r2 - x2) = 0
x = r / √2 [ oder x = - r / √2 ]
Dle Länge des Rechtecks mit maximalem A beträgt also 2x = √2·r
und die Breite √(r2 - x2) = √(3/4*r2) = r·√3 / 2
----------------
Der Umfang ergibt sich durch analoge Rechnung aus
U(x,y) = 4x + 2y
Gruß Wolfgang